KöMaL Problems in Physics, September 2014
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on October 10, 2014. |
M. 343. Measure the damping of a pendulum, which has a 50 g bob suspended ``bifilarly'' by two threads. The pendulum is released from the horizontal. Measure and plot the period of the pendulum, and the angle of its maximum displacement as a function of the number of swings.
(6 pont)
 |
Problems with sign 'P'Deadline expired on October 10, 2014. |
P. 4649. We observe the full Moon with a telescope. Somebody shades half of the objective lens in fun. What kind of change can be observed in the image of the telescope?
(3 pont)
P. 4650. There is a mixture of 12 grams Helium and 16 grams Oxygen in a 25-litre bottle. What is the density and the pressure of this gas at a temperature of 27 \(\displaystyle {}^\circ\)C?
(3 pont)
P. 4651. A wedge is driven into a log. The angle at the thin end of the wedge is \(\displaystyle 24^\circ\). What is the least value of the coefficient of static friction between the wedge end the wooden log, if the wedge gets stuck in the log?
(4 pont)
P. 4652. The voltage measured between points \(\displaystyle A\) and \(\displaystyle B\) in the circuit consisting of eight resistors, each having a resistance of \(\displaystyle 100~\Omega\), is \(\displaystyle 50~V\).
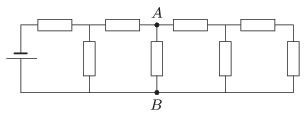
What is the power dissipated in the system of eight resistors?
(4 pont)
P. 4653. There is a small (point-like) object at the topmost point of a fixed sphere of absolutely smooth surface. If this object is slightly displaced from its equilibrium position it slides frictionlessly along the surface of the sphere for a while, and then leaving the sphere it falls down.
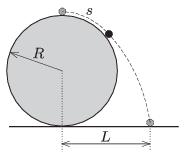
\(\displaystyle a)\) How much distance is covered by the small object along the surface of the sphere until it leaves the sphere?
\(\displaystyle b)\) Measured from the vertical diameter of the sphere, at what distance \(\displaystyle L\) will the object hit the horizontal surface?
The radius of the sphere is \(\displaystyle R=1.5\) m.
(4 pont)
P. 4654. What is the least force that must be applied in order to overturn an ice cube skidding on ice? (Friction is negligible.)
(4 pont)
P. 4655. A piece of thread is wound around the rim of a very light disc if radius \(\displaystyle r=0.1\) m. An object of mass \(\displaystyle m=100\) g is attached to the free end of the thread. The disc has a horizontal axle at its centre and also there is a rod of negligible mass fixed to it. There is a small object of mass \(\displaystyle M\) attached to the end of the rod at a distance of \(\displaystyle R=0.2\) m from the centre of the disc.
Initially the system is at rest in the position shown in the figure. Suddenly the support of the object of mass \(\displaystyle m\) is taken away, and the small object of mass \(\displaystyle M\) just reaches the position indicated by the broken line, enclosing a \(\displaystyle 60^\circ\) angle with the vertical. After some lightly damped swings the rod reaches its equilibrium position, at which the angle between the rod and the vertical is \(\displaystyle \varphi\).
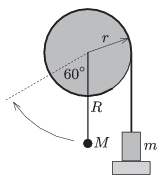
\(\displaystyle a)\) What is the mass \(\displaystyle M\) of the object at the end of the rod?
\(\displaystyle b)\) What is the measure of the angle \(\displaystyle \varphi\)?
\(\displaystyle c)\) If the system is displaced a bit from its equilibrium position, what is the period of the oscillation?
(5 pont)
P. 4656. Three threads of equal length are hung at the same point and at the other end of each thread there is a small sphere, each having the same mass. The same charge is given to each of them. What is the radius of the circle at which the spheres are at rest?
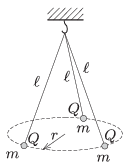
Data: \(\displaystyle \ell=20\) cm, \(\displaystyle m=1.3~\)grams, \(\displaystyle Q=1.2\cdot10^{-7}\) C.
(5 pont)
P. 4657. A thermally insulated cylinder of cross section 1 dm\(\displaystyle {}^2\), containing some air, is attached to the ceiling. Initially the volume of the air is 3 litres, and its temperature is 300 K. The piston which confines the gas into the cylinder is also thermally insulated and has a mass of 10 kg. Another 10-kg object is attached with a rope to the piston and hangs 10 cm above the ground. The air is slowly heated until its volume reaches the value of 4.4 litres.
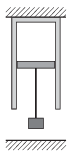
\(\displaystyle a)\) What is the temperature of the gas at the final state?
\(\displaystyle b)\) How much heat should be added to the gas?
(5 pont)
P. 4658. How many neutrons arise one day from one nuclear reactor at Paks, and from the nuclear training reactor of the Budapest University of Technology and Economy (BME)? (Suppose that both reactors are operated continuously for 24 hours.)
Data: The thermal power of one reactor at Paks is 1485 MW, and the maximum thermal power of the training reactor at the Budapest University is 100 W. During one fission 185 MeW is released and the average of the arising neutrons during one fission is 2.43.
(3 pont)
P. 4659. Inside a thin shell hollow metal sphere of radius 20 cm there is a metal ball of radius 10 cm. The centres of the ball and the sphere coincide. The inside ball is earthed with a very long wire, which is led through a small hole in the outer sphere. The outer sphere is given a charge of \(\displaystyle 10^{-8}\) C. What will the potential of the outer sphere be?
(6 pont)
Upload your solutions above.
