Ez itt a cím helye

Matematika feladatok megoldása

B. 3677. Határozzuk meg mindazokat a pozitív egészekből álló ($\displaystyle \alpha$;$\displaystyle \beta$) számpárokat, amelyekre a pozitív egészek halmazát fel lehet bontani két diszjunkt halmazra, A-ra és B-re úgy, hogy {$\displaystyle \alpha$a |a$\displaystyle \in$A}= {$\displaystyle \beta$b|b$\displaystyle \in$B} teljesüljön. (4 pont)

IMC10, Kolozsvár, 2003

I. megoldás. Az egyszerűség kedvéért a továbbiakban azt a számhalmazt, amely egy H számhalmaz elemeinek a k-szorosából áll, kH-val jelöljük. A feladat feltétele így $\displaystyle \alpha$A =$\displaystyle \beta$B, miközben az $\displaystyle \frac{1}{\beta}\alpha A=B$ és az $\displaystyle \frac{1}{\alpha}\beta B=A$ halmazok a pozitív egészek közös elem nélküli előállítását adják. Megmutatjuk, hogy a megfelelő számpárok olyanok, hogy egyikük a másik valódi osztója, továbbá ezek mind megfelelőek.

Először azt látjuk be, hogy a nem ilyen tulajdonságú számpárokra nem valósítható meg a pozitív egészek megfelelő szétválasztása. Elsőként legyen $\displaystyle \alpha$=$\displaystyle \beta$. Ilyenkor nyilván nem valósítható meg a kívánt szétosztás, hiszen ekkor az $\displaystyle \alpha$A = $\displaystyle \beta$B egyenlőségből az A és B halmazok egyenlősége következik. A szimmetria miatt ezután föltehető, hogy $\displaystyle \alpha$< $\displaystyle \beta$, és persze, ha ($\displaystyle \alpha$;$\displaystyle \beta$) jó számpár, akkor ($\displaystyle \beta$;$\displaystyle \alpha$) is az.

Nyilvánvaló, hogy ha k tetszőleges pozitív egész és ($\displaystyle \alpha$;$\displaystyle \beta$) jó számpár, akkor (k$\displaystyle \alpha$; k$\displaystyle \beta$) is az, hiszen a megadott halmazok csak k-val szorzódnak. Ennek a tulajdonságnak a megfordítása is igaz: ha k a jó ($\displaystyle \alpha$;$\displaystyle \beta$) közös osztója, akkor az $\displaystyle \left(\frac{\alpha}{k};\frac{\beta}{k}\right)$ számpár is jó. Ezek szerint elegendő megtalálni a relatív prím jó számpárokat.

Legyen tehát ($\displaystyle \alpha$;$\displaystyle \beta$) = 1, és tegyük fel, hogy 1$\displaystyle \in$A. Ekkor $\displaystyle \alpha$^.1=$\displaystyle \alpha$ $\in$ $\alpha$ A. Mivel ennek a halmaznak minden eleme $\beta$ b alakban is előáll, azért $1\notin B$ miatt $\alpha$ legalább 2 $\beta$ . Ez viszont nem lehetséges, hiszen föltevésünk szerint $\alpha$ < $\beta$ . Így csak 1 $\in$ B lehetséges. Ekkor $\beta$ ^.1= $\beta$ $\in$ $\beta$ B= $\alpha$ A, azaz $\beta$ az $\alpha$ többszöröse. Mivel feltettük, hogy relatív prímek, ez csak úgy lehetséges, ha $\alpha$ =1. Ezzel tehát beláttuk, hogy a relatív prím $\alpha$ < $\beta$ megoldásokra $\alpha$ = 1, $\beta$ > 1 szükséges.

Most megmutatjuk, hogy ez elégséges is, minden ilyen számpárhoz létezik megfelelő felosztás. Egyszerűen megadjuk a kívánt tulajdonságú halmazokat. Legyenek A elemei az m^. $\beta$ ^2k+1 alakú számok, ahol k tetszőleges nemnegatív egész, és m olyan egész szám, amit $\beta$ már nem oszt. Az m^. $\beta$ ^2k alakú számok pedig legyenek B elemei. A számelmélet alaptétele szerint így minden pozitív egész a két halmaz közül pontosan az egyikbe került, továbbá a B halmaz elemeit $\beta$ -val szorozva valóban az A-beli elemeket kapjuk és megfordítva. (Továbbra is $\alpha$ =1.)

A jó relatív prím számpárok tehát valóban olyanok, hogy ( $\alpha$ ; $\beta$ ) egyike 1, másika 1-nél nagyobb tetszőleges egész. Az összes megfelelő számpár pedig az ilyenek pozitív egész többszörösei, tehát azok, ahol a számpár egyik tagja valódi osztója a másiknak.

Erdélyi Márton (Fazekas M. Fővárosi Gyak. Gimn., 10. évf.) dolgozata alapján

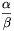II. megoldás. $\alpha$ = $\beta$ -t az előző megoldás szerint kizárhatjuk. Legyen $\frac{\alpha}{\beta}$ először 1-nél nagyobb egész szám; megmutatjuk, hogy ilyenkor van megfelelő szétosztás. A következő algoritmus szerint haladjunk sorra a pozitív egész számokon: ha a soron következő k számot még nem helyeztük el, akkor tegyük az A-ba, az 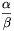$\frac{\alpha}{\beta}$ -szorosát pedig a B-be. Ez azt jelenti, hogy első lépésben az 1, ami természetesen még nem került helyre, az A-ba kerül, 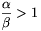$\frac{\alpha}{\beta}>1$ pedig B-be. Az eljárás egyértelmű, és minden pozitív szám bekerül a két halmaz egyikébe. Mivel ezzel 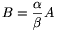$B=\frac{\alpha}{\beta}A$ , nyilván teljesül a feladatban előírt $\alpha$ A = $\beta$ B egyenlőség. 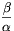(Érdemes meggondolni, milyen algebrai tulajdonságai vannak a halmaz számmal való szorzása műveletnek.) Hasonlóan adódik a felosztás, ha $\frac{\beta}{\alpha}$ 1-nél nagyobb egész.

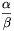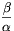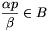Még azt kell megmutatnunk, hogy ha sem $\frac{\alpha}{\beta}$ , sem $\frac{\beta}{\alpha}$ nem egész, akkor nincsen megfelelő szétosztás. Legyen p olyan prím, amely sem $\alpha$ -nak, sem pedig $\beta$ -nak nem osztója. Ha lenne megfelelő szétosztás, akkor p-nek is ott kellene lennie az egyik halmazban, például A-ban. Ekkor $\alpha$ ^.p $\in$ $\alpha$ A= $\beta$ B, tehát $\frac{\alpha p}{\beta}\in B$ . Ez viszont nem lehetséges, hiszen feltevésünk szerint $\beta$ és $\alpha$ p relatív prímek, tehát ez a tört nem egész szám. Hasonlóan kapjuk, hogy p a B halmazban sem lehet.

Szabó Botond (Szeged, SZTE Ságvári Endre Gyak. Gimn., 12. évf.) dolgozata alapján

<<\small>>71 dolgozat érkezett. 4 pontos: Ablonczy Dávid, Birkner Tamás, Birkus Róbert, Bitai Tamás, Czank Tamás, Erdélyi Márton, Fehér Gábor, Filus Tamás, Gehér György, Gyenizse Gergő, Hegyháti Máté, Hujter Bálint, Koszta Botond, Kunovszki Péter, Kutas Péter, Nagy Csaba, Nagy-Baló András, Pálinkás Csaba, Stippinger Marcell, Strenner Balázs, Szabó Botond, Szabó Tamás, Szalkai Balázs, Szalóki Dávid, Szilágyi Dániel, Sziroczák Richárd, Ureczky Bálint, Vadász Gergely, Vass Márton megoldása. 3 pontos 19, 2 pontos 10, 1 pontos 9, 0 pontos 4 dolgozat.

B. 3677. - a javító tapasztalatai

A feladat két részből állt: meg kellett mondani, hogy milyen ( $\alpha$ ; $\beta$ ) párok jók (és ezekre konstrukciót adni), továbbá meg kellett mutatni, hogy csak ezek jók (azaz másféle számpárokra nincs megfelelő szétosztás). A feladat 4 pontot ért, 2-2 pontot lehetett kapni ezen részfeladatokért. Nézzük meg jobban ezt a két részt:

1. Annak igazolása, hogy csak az olyan különböző számokból álló párok jók, ahol a nagyobbik a kisebbik többszöröse: a legkönnyebben azok tudták elintézni a kérdést, akik az első megoldás megoldójához hasonlóan rájöttek, hogy az 1 szám elhelyezését kell vizsgálni. Lényegében ilyesmi történik a II. megoldásban is, csak ott 1 helyett egy másik olyan szám elhelyezését vizsgáljuk, amely az $\alpha$ $\beta$ szorzattal relatív prím.

Ez a rész egy komoly hibalehetőséget is rejt: többen azért kaptak 3 pontot, mert csak azt hozták ki, hogy $\alpha$ osztója $\beta$ -nak vagy megfordítva, arról viszont megfeledkeztek, hogy a két számnak különbözőnek kell lennie. Ha jobban odafigyelnek a második részben, mit is használnak valójában, akkor legkésőbb itt kiderülhetett volna, hogy a két szám nem lehet egyenlő, a hányadosuknak nem csak egésznek, hanem 1-nél nagyobbnak is kell lennie. 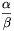Érdemes tehát odafigyelni, hogy ha egy megoldásban egy paraméter a főszereplő (mint most az $\frac{\alpha}{\beta}$ hányados, illetve a reciproka), akkor gondosan meg kell vizsgálni a paraméter értékkészletét, különös tekintettel a speciális értékekre, amikor a paraméter nem úgy működik, mint az általános esetben.

2. Konstrukció. A II. megoldás során olyan konstrukciót adtunk, ahol sorra ,,bepakoltuk'' a számokat az egyik vagy a másik halmazba. Maga a felbontás éppen az lesz, amit az I. megoldás szerzője talált, a két konstrukció lényegében azonos. A konkrét elrendezés megadása persze elegánsabbnak tűnhet, a II. megoldás viszont többet árul el arról, hogyan lehet erre rájönni, illetve arról, hogy lényegében miért csak ez az egy konstrukció lehetséges.

Voltak, akik olyan konstrukcióval próbálkoztak, hogy - az (1; $\beta$ ) esetben - a $\beta$ -val osztható számokat rakták az A, a többi számot pedig a B halmazba. Ekkor azonban $\beta$ ²-hez nem lenne megfelelő B-beli b elem úgy, hogy $\beta$ ² = $\beta$ b. Közelebb jutott a valódi konstrukcióhoz az, aki $\beta$ minden páros kitevőjű hatványát az egyik halmazba tette (ezért 1 pont járt ebből a feladatrészből), ám a páros kitevőjű hatványok $\beta$ -val nem osztható többszöröseiről elfeledkezett. Az itt elkövetett hibákat még egyszerűbb kiszűrni: ehhez csak lelkiismeretesen kell ellenőrizni, hogy a javasolt konstrukcióra teljesülnek-e a feltételek.

Tábor Áron

egyetemi hallgató, ELTE TTK

Már regisztráltál?
Új vendég vagy?