Kádár Csilla:

Szappanhártyák

Recept

Végy egy tálat. Önts bele 1 dl vizet, 1 dl glicerint (gyógyszertárakban kapható) és 1 teáskanál mosogatószert (a legolcsóbb a legjobb, abban nincs kézkímélő, ami gátolná a hártyaképződést). Miután összekeverted ezeket, márts bele egy fém teásdobozt! Figyeld meg, hogyan változnak a létrejövő függőleges hártyán a színek! Ha úgy érzed, most már tudod, hogy ,,mi történik'' egy szappanhártyán, akkor íme egy másik recept: 2 dl víz, 1 teáskanál mosogatószer és 2 teáskanál méz. Ez a ,,mézes hártya'' receptje. Készíthetsz olyan szappanhártyát is, amely annyira gyorsan kavarog, hogy az egyes színek már nem is láthatók. Ekkor 1 dl vízhez csak 2-3 teáskanál glicerint és 1-2 teáskanál mosogatószert kell tenned! Természetesen te is kitalálhatsz recepteket!

A szappanhártya színei

A fény hullámhosszával (400-800 nm) összemérhető vastagságú szappanhártyára eső fény kis része (4%) visszaverődik, mégpedig egy része a hártya első felületéről, más része a hártya hátsó felületéről. A két közeli felületről visszavert fény találkozásakor (interferenciájakor) egyes hullámok erősödnek, mások gyengülnek. Ennek következtében lesz a visszavert fény színes. Az, hogy mely hullámok erősödnek illetve gyengülnek, függ a hártya vastagságától. Így a visszavert fény színeiből kiszámíthatjuk, hogy körülbelül milyen vastag lehet egy piros színű csík a hártyánkon.

1. ábra

Essen $\displaystyle lambda$ hullámhosszúságú (monokromatikus) fény a t vastagságú lemezre $\displaystyle alpha$ szög alatt (1. ábra). Az A-ban és C-ben megjelenő sugarak interferenciájára vagyunk kíváncsiak: ehhez a találkozó hullámok közötti $Delta$ s optikai útkülönbséget (a törésmutatóval súlyozott utak különbségét) kell meghatároznunk. Ha a levegő törésmutatóját 1-nek, a hártyáét n-nek vesszük, akkor

$\displaystyle \Delta s=n(AB+BC)-AH=\frac{2nt}{\cos\beta}-AC\sin\alpha,$

ahol $\displaystyle AH\bot CH$. Felhasználva a

sin$\displaystyle alpha$=nsin$\displaystyle beta$ és $\displaystyle AC=2t\mathop{\rm tg}\beta$

összefüggéseket az optikai útkülönbségre (pontosabban annak a geometriai távolságoktól függő részére)

$\displaystyle \Delta s=\frac{2nt}{\cos\beta}-\frac{2nt}{\cos\beta}\sin^2\beta=2nt\cos\beta$

adódik. Vegyük még azt is figyelembe, hogy optikailag sűrűbb közeg határfelületéről való visszaverődéskor $\displaystyle pi$ fázisugrás lép fel (a ,,hullámhegy'' ,,hullámvölgyként'' verődik vissza), amely $\frac{\lambda}{2}$ optikai útkülönbségnek felel meg [1], így végül

$\displaystyle \Delta s=2nt\cos\beta-\frac{\lambda}{2}.$

Merőleges beesés ($\displaystyle beta$=0) esetén az útkülönbség a 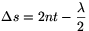$\Delta s=2nt-\frac{\lambda}{2}$ összefüggéssé egyszerűsödik.

Hullámok találkozásakor, ha az optikai útkülönbség $Delta$ s=k$\displaystyle lambda$ (k=0,1,2,...), maximális erősítés, ha pedig $\displaystyle \Delta s=\left(k-\frac{1}{2}\right)\lambda$, akkor maximális gyengítés lép fel. Maximális erősítés esetén tehát

$\displaystyle 2nt=\left(k+\frac{1}{2}\right)\qquad(k=0,1,2,\dots),$

míg maximális gyengítésnél pedig

2nt=k$\displaystyle lambda$ (k=0,1,2,...)

teljesül. A k paramétert az interferencia rendjének nevezzük.

A szappanhártya t vastagságát k és $lambda$ függvényében a fenti összefüggéseknek megfelelően táblázatba rendezhetjük.

szín	hullámhossz ()	hártyavastagság (t)
		maximális erősítés		maximális gyengítés
		k=0	k=1	k=0	k=1	k=2
piros	680 nm	120 nm	362 nm	0 nm	241 nm	482 nm
narancs	590 nm	104 nm	314 nm	0 nm	209 nm	418 nm
sárga	580 nm	103 nm	309 nm	0 nm	206 nm	411 nm
zöld	530 nm	94 nm	282 nm	0 nm	188 nm	376 nm
kék	470 nm	83 nm	250 nm	0 nm	167 nm	333 nm
lila	405 nm	71 nm	215 nm	0 nm	144 nm	287 nm

A táblázatból látszik, hogy t$\displaystyle ll$ $lambda$ esetén az interferencia minden hullámhosszra gyengítést ad, ezért a hártyát ekkor feketének látjuk. Ez az úgynevezett Newton-féle fekete hártya. Más hártyavastagságok interferenciaszínét is megbecsülhetjük. Milyen színű lesz a hártya például t $approx$ 370 nm esetén? 362 nm-nél a piros színben maximális erősítés, 376 nm-nél zöld színben maximális gyengítés van - így 370 nm-nél a zöld szín komplementerét (kiegészítő színét), a pirosat fogjuk látni. Mivel piros színben még erősítés is fellép, ezért ilyen vastagság mellett a hártya élénk piros színben fog pompázni. Ez csak becslés, hiszen nem vettük figyelembe a fehér fény többi komponensének hatását.

Pontosabb adatokat a szappanhártya felületéről visszavert fény intenzitásának mérésével kaphatunk. Lawrence a következő táblázatba foglalta össze mérési eredményeit [2]:

szín	rend	hártyavastagság
fekete	0	6-12 nm
ezüstfehér	0	150 nm
borostyánsárga	0	?
bíborvörös	0	201 nm
lila	1	216 nm
kék	1	250 nm
zöld	1	290 nm
sárga	1	322 nm
narancs	1	348 nm
karmazsinpiros	1	371 nm
bordó	2	396 nm
kék	2	410 nm
kék	2	428 nm
smaragdzöld	2	466 nm
sárgászöld	2	502 nm

A hátsó belső borítón egy függőleges helyzetű szappanhártya különböző időpontokban készített fényképfelvételei láthatók. Az oldat az első (méz nélküli) recept szerint készült, és a hártyán (amely akár 5-6 órán át is megmaradhat) látványos színes csíkrendszer alakult ki. A legutolsó (legkésőbb) készült fényképen látható hártya teteje már annyira elvékonyodott, hogy ott hullámhossztól függetlenül csak a nulladrendű kioltás feltétele teljesül (Newton-hártya), emiatt az koromfekete.

A hártya vastagsága - amely időben és térben (a magasság szerint) egyaránt változik - a fenti táblázatok alapján megbecsülhető. Vajon megjósolható-e, hogy bizonyos idejű (például 3 óra) várakozás után - feltételezve, hogy ,,él'' még - milyen színű lesz a hártya? A kérdés megválaszolásához vizsgáljuk meg kicsit részletesebben a hártya elvékonyodásának folyamatát!

Függőleges helyzetű hártyában a folyadék saját súlyának hatására lefelé áramlik. Ennek eredményeképpen a hártya vastagsága felülről lefelé fokozatosan nő. Hogyan becsülhető meg a változás? Ha figyelmen kívül hagyjuk a párolgás hatását, akkor - a hártya felületét két merev falnak gondolva - lényegében párhuzamos síklemezek közti viszkózus folyást kell vizsgálnunk [3]. A folyadék belsejében súrlódás van, így a gyorsabban mozgó folyadékrétegek a szomszédos, lassabban mozgó rétegeket gyorsítani, az utóbbiak pedig a gyorsabban mozgó rétegeket lassítani igyekeznek. A gyorsító illetve lassító erőket a Newton-féle súrlódási törvény írja le [1].

2. ábra

Jelöljük x-szel a szappanhártya közepétől mért távolságot, v(x)-szel az x helyen a folyadék sebességét ( 2. ábra). Tekintsük a hártya közepétől x távolságra lévő két - szimmetrikusan elhelyezkedő - vékony folyadékréteget. A két folyadékréteg között elhelyezkedő 2x széles folyadékoszlopra felírva Newton mozgástörvényét, a következőt kapjuk:

mg+2F_s=ma.

A Newton-féle súrlódási törvénynek megfelelően az egyik (x távolságra lévő) folyadékréteg által a folyadékoszlopra ható erő 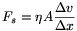$F_{s}=\eta A\frac{\Delta v}{\Delta x}$ . Egyenletes áramlást feltételezve a=0, ezért

$mg+2\eta A\frac{\Delta v}{\Delta x}=0,$

ahol A a besatírozott rész területe, 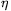$eta$ a folyadék viszkozitása, m pedig a $varrho$ sűrűségű folyadékoszlop tömege: m=V $rho$ =2xA $rho$ . Így

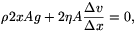
$\rho2xAg+2\eta A\frac{\Delta v}{\Delta x}=0,$

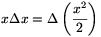ahonnan $x\Delta x=\Delta\left(\frac{x^2}{2}\right)$ felhasználásával

$rho$ xg $Delta$ x=- $eta$ $Delta$ v

adódik. A fenti kifejezést összegezve x' távolságtól a hártya széléig, figyelembe véve, hogy a folyadék sebessége a merev fal mentén nulla, a következőt kapjuk:

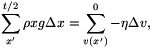
$\sum_{x'}^{t/2}\rho xg\Delta x=\sum_{v(x')}^0-\eta\Delta v,$

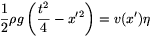
$\frac{1}{2}\rho g\left(\frac{t^2}{4}-x'^2\right)=v(x')\eta$

összefügés adódik, amelyből v(x') sebesség kifejezhető:

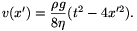
$v(x')=\frac{\rho g}{8\eta}(t^2-4x'^2).$

A sebesség ismeretében már könnyen kiszámítható a hosszegységre eső folyadék-hozam, vagyis a hártya egységnyi széles szakaszán időegység alatt átfolyt folyadék Q térfogata. Vizsgáljuk a hártya középétől x távolságra lévő $Delta$ x vastag folyadékrétegeket. Legyen a hártya l széles. Ekkor az időegység alatt átfolyt folyadék mennyisége a kérdéses szakaszokon:

$Delta$ I=2v(x)l $Delta$ x,

a teljes hozam tehát:

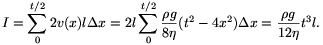
$I=\sum_0^{t/2}2v(x)l\Delta x=2l\sum_0^{t/2}\frac{\rho g}{8\eta}(t^2-4x^2)\Delta x=\frac{\rho g}{12\eta}t^3l.$

Ebből a 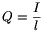$Q=\frac{I}{l}$ miatt

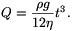
$Q=\frac{\rho g}{12\eta}t^3.$

A hozam tehát a hártya vastagságának köbével arányos, de mivel a vastagság helyről helyre és időben is változik, t=t(z, $tau$ ), és így a hozam is hely- és időfüggő lesz: Q=Q(z, $tau$ ). ( $tau$ a hártya létrehozása óta eltelt időt jelöli.) Ha a z tengelyt lefelé irányítjuk, és képezzük a Q=Q(z+ $Delta$ z, $tau$ )-Q(z, $tau$ ) különbséget, az nyilván megadja egy $Delta$ z vastagságú sávból kifolyó többletfolyadék térfogatát. Ennek folyadékhiánynak együtt kell járnia a hártya elvékonyodásából származó térfogatcsökkenéssel, ami viszont a t(z, $tau$ )-t(z, $tau$ + $Delta$ $tau$ ) különbséggel arányos. A kétféle módon kiszámított térfogatváltozás egyenlősége meghatározza a falvastagság változási ütemét, és (itt most nem részletezhető számítás után) a következő eredményre vezet:

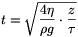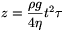$t=\sqrt{\frac{4\eta}{\rho g}\cdot{z\over\tau}}$ , azaz $z=\frac{\rho g}{4\eta}t^2\tau$ .

Közvetlenül a hártya képződése után ( $tau$ =0-kor) a hártya vastagsága formálisan végtelen, ami arra figyelmeztet, hogy ekkor a levezetés során alkalmazott megfontolások valamelyike nem érvényes. Később, amikor a számítás eredményét elfogadhatónak tartjuk, $z\propto t^2$ , tehát a szappanhártya keresztmetszete parabola alakot ölt.

Elméleti megfontolásainkat ellenőrizhetjük az intenzitásméréssel kapott táblázat segítségével, amelyből a szappanhártya vastagsága megbecsülhető. A mérési adatokból jól látszik, hogy a hártya keresztmetszete az idő múlásával egyre inkább felveszi a parabola alakot, habár az elméleti számítások szerint a hártyának körülbelül kétszer-háromszor olyen vastagnak kellene lennie, mint a ténylegesen megfigyelt.

Buborékokkal is végezhető hasonló kísérlet, de ott a színek változását már sokkal nehezebb megfigyelni, mert a buborék egyben tükörként is működik: leképezi a környezetét. A fém teásdobozos kísérletnél a doboz belsejének tükröző hatását elkerülhetjük, ha matt fekete papírral béleljük ki.

Jó kísérletezést!

Irodalom

[1] Budó Á.: Kísérleti fizika I, III, Tankönyvkiadó, Budapest, 1986.

[2] A. S. C. Lawrence: Soap Films, Bell, 1929.

[3] K. Mysels, K. Shinoda, S. Frankel: Soap Films. Studies of their thinning, Pergamon Press, London, 1959.

[4] Rajkovits Zs. - Főzy I.: Színes szappanhártyák, Természet világa, 1992/május.

Zs. Rajkovits: Soap Films and Soap Bubbles in Physics Education, Physics & Technology Quest, 1997 December.

Már regisztráltál?
Új vendég vagy?