Az A. 486. feladat (2009. szeptember)

A. 486. Jelöljük 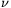$\nu$ (n)-nel a 2 kitevőjét az n! prímtényezős felbontásában. Mutassuk meg, hogy tetszőleges a és m pozitív egészekhez létezik olyan n>1 egész szám, amire $\nu(n) \equiv a \pmod{m}$ .

(5 pont)

A beküldési határidő 2009. október 12-én LEJÁRT.

Megoldás. Felhasználjuk, hogy

$\nu(n) = \sum_{k=1}^\infty \bigg[\frac{n}{2^k}\bigg];$

(1)

ez speciális esete az úgynevezett Legendre-formulának. (A Legendre-formuláról bővebben lást az 1. megjegyzést.)

Ha az n szám kettes számrendszerbeli alakja $n=\overline{d_\ell d_{\ell-1}\ldots d_1d_0} = \sum\limits_{i=0}^\ell d_i\cdot2^i$ , ahol a $d_0,\ldots,d_\ell$ számjegyek mindegyike 0 vagy 1, akkor (1)-ben csak k $\le$ $\ell$ esetén kapunk 0-tól különböző tagokat, és

$\nu(n) = \sum_{k=1}^\infty \bigg[\frac{n}{2^k}\bigg] = \sum_{k=1}^\ell \Bigg[\frac{\overline{d_\ell d_{\ell-1}\ldots d_1d_0}}{2^k}\Bigg] = \sum_{k=1}^\ell \overline{d_\ell d_{\ell-1}\ldots d_k} =$

$= \sum_{k=1}^\ell \left(\sum_{i=k}^\ell d_i \cdot 2^{i-k}\right) = \sum_{i=1}^\ell d_i \left(\sum_{k=1}^i 2^{i-k}\right) = \sum_{i=1}^\ell d_i \cdot (2^i-1).$

Ennek egyszerű következménye, hogy pontosan azok a pozitív egészek állnak elő 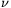$\nu$ (n) alakban, amelyek felírhatók különböző 2ⁱ-1 alakú számok összegeként.

Következő lépésként megmutatjuk, hogy van olyan r szám, ami relatív m-mel, és végtelen sokszor áll elő 2ⁱ-1 alakú számok m-mel való osztási maradékaként, vagyis léteznek olyan $i_1<i_2<i_3<\ldots$ pozitív egészek, amelyekre

$2^{i_1}-1 \equiv 2^{i_2}-1 \equiv 2^{i_3}-1 \equiv \ldots \equiv r \pmod{m}.$

Írjuk m-et 2^tu alakban, ahol u páratlan szám, és tekintsünk egy tetszőleges olyan i $\ge$ t pozitív egészt, amire i-1 osztható $\varphi$ (u)-val. Nyilván végtelen sok ilyen i létezik. Az Euler-Fermat-tétel alapján minden egyes ilyen i értékre

$u \,\Big|\, 2^{\varphi (u)}-1 \,\Big|\, 2^{i-1}-1,$

$2^i-1 = 2(2^{i-1}-1) + 1 \equiv 1 \pmod{u},$

(2)

és i $\ge$ t miatt

$2^i-1 \equiv -1 \pmod{2^t}.$

(3)

A 2ⁱ-1 szám (2) és (3) miatt relatív prím u-val és 2^t-vel is, továbbá (2) és (3) egyértelműen meghatározza 2ⁱ-1 maradékát modulo [u,2^t]=m. Ez a maradék tehát valóban végtelen sokszor előfordul.

Mivel m és r relatív prímek, az $r,2r,3r,\ldots$ számok teljes maradékrendszert alkotnak modulo m, és létezik olyan u pozitív egész, amire $a\equiv ur\pmod{m}$ . Ekkor az $n=2^{i_1}+\ldots+2^{i_u}$ számra

$\nu(n) = \nu\big( 2^{i_1}+\ldots+2^{i_u} \big) = (2^{i_1}-1)+\ldots+(2^{i_u}-1) \equiv u\cdot r \equiv a \pmod{m}.$

Ezzel megkonstruáltuk a kívánt n számot.

Éles András (Debrecen, Fazekas M. Gimn., 12. o. t.) dolgozata alapján

Megjegyzések. 1. Ha 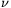$\nu$ _p(n)-nel jelöljük tetszőleges p prímszámra és nemnnegatív egész n-re a p kitevőjét az n! prímtényezős felbontásában, akkor az úgynevezett Legendre-formula szerint

$\nu_p(n) = \bigg[\frac{n}{p}\bigg] + \bigg[\frac{n}{p^2}\bigg] + \bigg[\frac{n}{p^3}\bigg] + \ldots = \sum_{k=1}^\infty \bigg[\frac{n}{p^k}\bigg].$

Ha összeszámoljuk azt, hogy az $1,2,\ldots,n$ számok között hány p-vel osztható, hány p²-tel osztható stb. van, éppen a jobboldalon álló összeget kapjuk. Ez szemléletesen bizonyítja a képletet.

A formálisabb bizonyításhoz tetszőleges $\ell$ pozitív egészre jelöljük $\mu$ _p( $\ell$ )-lel a p kitevőjét az $\ell$ prímtényezős felbontásában. Mivel szorzásnál a kitevők összeadódnak,

$\nu_p(n) = \mu_p(1\cdot2\cdot\ldots\cdot n) = \mu_p(1) + \mu_p(2) +\ldots+ \mu_p(n).$

Tekintsük most az összes olyan (k, $\ell$ ) párt, amelyekben 1 $\le$ $\ell$ $\le$ n és p^k osztója $\ell$ -nek, és számoljuk össze kétféleképpen az ilyen tulajdonságú párokat.

Először csoportosítsuk a (k, $\ell$ ) párokat $\ell$ értékei szerint. Egy rögzített $\ell$ szám a p-nek mindig pontosan $\mu$ _p( $\ell$ ) különböző hatványával osztható: ezek a $p,p^2,\ldots,p^{\mu_p(\ell)}$ számok, ezért

$\sum_{(k,\ell)} 1 = \sum_{\ell}^n \sum_{p^k|\ell} 1 = \sum_{\ell}^n \mu_p(\ell) = \nu_p(n).$

(4)

Most csoportosítsuk a párokat k értékei szerint. Minden egyes k-ra azokat az $\ell$ -eket keressük, amelyek többszöresei p^k-nak; az $1,2,\ldots,n$ között ezek száma $\displaystyle\bigg[\frac{n}{p^k}\bigg]$ . A párok száma tehát

$\sum_{(k,\ell)} 1 = \sum_{k=1}^\infty \, \sum_{\ell\le n, ~ p^k|\ell} 1 = \sum_{k=1}^\infty \, \bigg[\frac{n}{p^k}\bigg].$

(5)

A (4) és (5) képletek együtt bizonyítják a Legendre-formulát.

2. Az állítást a 2 helyett bármelyik másik prímmel kimondhatjuk; a bizonyítás minden nehézség nélkül átírható.

Statisztika:

13 dolgozat érkezett.

5 pontot kapott: Ágoston Tamás, Backhausz Tibor, Bodor Bertalan, Éles András, Frankl Nóra, Nagy 235 János, Nagy 648 Donát, Somogyi Ákos, Strenner Péter, Szabó 928 Attila.

4 pontot kapott: Kalina Kende.

3 pontot kapott: 1 versenyző.

0 pontot kapott: 1 versenyző.

A KöMaL 2009. szeptemberi matematika feladatai

13 dolgozat érkezett.
5 pontot kapott:	Ágoston Tamás, Backhausz Tibor, Bodor Bertalan, Éles András, Frankl Nóra, Nagy 235 János, Nagy 648 Donát, Somogyi Ákos, Strenner Péter, Szabó 928 Attila.
4 pontot kapott:	Kalina Kende.
3 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

Már regisztráltál?
Új vendég vagy?