 |
Az A. 547. feladat (2011. november) |
A. 547. Adott az OA1A2A3 tetraéder mindegyik OAi élén egy Bi belső pont, az OAi él Ai-n túli meghosszabbításán pedig egy Ci pont (i=1,2,3). Tegyük fel, hogy az OAi+1Ai+2 és BiAi+1Ai+2 síkok által határolt hat lapú testbe, továbbá az BiAi+1Ai+2 és CiAi+1Ai+2 síkok által határolt testbe is egy-egy gömböt lehet írni. Bizonyítsuk be, hogy ekkor az OAi+1Ai+2 és CiAi+1Ai+2 síkok által határolt testbe is gömböt lehet írni.
(5 pont)
A beküldési határidő 2011. december 12-én LEJÁRT.
Megoldásvázlat. A bizonyítás során irányított egyenesekel, irányított síkokkal és ezek irányított szögeivel fogunk dolgozni. Tetszőleges, nem kollineáris X,Y,Z pontok esetén az XY egyenes pozitív iránya megegyezik az vektor irányával, az XYZ sík pozitív oldalára (a jobbkézszabálynak megfelelően) az
vektor mutat.
Lemma. Legyen  irányított egyenes, amire illeszkednek a
irányított egyenes, amire illeszkednek a ,
és
irányított síkok. Legyen
az az irányított szög, amellyel
-t az
 körül a jobbkézszabály szerinti irányban
körül a jobbkézszabály szerinti irányban -be forgathatjuk (i=1,2; ezeket a szögeket modulo 360o értjük). Legyen X olyan pont, amelynek előjeles távolsága a
,
,
síkoktól rendre d, r, illetve -r. Ekkor a következők teljesülnek:
és
.
Bizonyítás. Legyen a
sík egységnyi hosszúságú normálvektora, ami a sík pozitív oldala felé mutat, és legyen
az
 szintén egységnyi irányvektora. Legyen
szintén egységnyi irányvektora. Legyen olyan vektor, ami
 egy pontját köti össze az X ponttal. Az X pont előjeles távolságát bármelyik
egy pontját köti össze az X ponttal. Az X pont előjeles távolságát bármelyik síktól
és
skaláris szorzataként kaphatjuk:
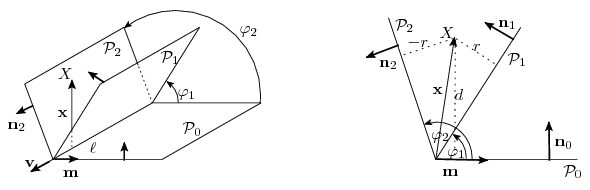
Legyen az
síkban
 -re merőleges egységvektor, amire
-re merőleges egységvektor, amire jobbsodrású rendszert alkot. Ekkor
Az -szel skalárisan szorozva,
sin  2.r-sin
2.r-sin  1.(-r)=sin (
1.(-r)=sin ( 2-
2- 1).d
1).d
Átrendezve,
Ezzel a lemmát igazoltuk.
Legyen az OAi+1Ai+2 és BiAi+1Ai+2 síkok által határolt testbe írt gömb középpontja X, sugara rX, előjeles távolsága az A1A2A3 síktól dX. Az X pont előjeles távolsága mindhárom BiAi+1Ai+2 síktól rX, és mindhárom OAi+1Ai+2 síktól -rX.
Hasonlóan, legyen a BiAi+1Ai+2 és CiAi+1Ai+2 síkok által határolt testbe írt gömb középpontja Y, sugara rY, Legyen Y előjeles távolsága az A1A2A3 síktól dY. Az Y pont előjeles távolsága mindhárom CiAi+1Ai+2 síktól rY, és mindhárom BiAi+1Ai+2 síktól -rY.
Minden egyes i=1,2,3-ra tekintsük az Ai+1Ai+2O és Ai+1Ai+2Ci irányított síkok külsö szögfelező síkját, és legyen Z a három szögfelező sík metszéspontja; ez lesz a keresett harmadik gömb középpontja. Egyelőre tegyük fel, hogy a három szögfelező sík egyike sem esik egybe az A1A2A3 síkkal; ebből következik, hogy Z nem eshet az A1A2A3 síkra. Legyen Z előjeles távolsága az A1A2A3 síktól , az A1A2C3 síktól
 . Mivel Z rajta van az A1A2C3 és A1A2O irányított síkok külső szögfelezőjén, Z távolsága az A1A2O irányított síktól -
. Mivel Z rajta van az A1A2C3 és A1A2O irányított síkok külső szögfelezőjén, Z távolsága az A1A2O irányított síktól - .
.
Legyen  =
= (A1A2A3,A1A2O),
(A1A2A3,A1A2O),  =
= (A1A2A3,A1A2B3) és
(A1A2A3,A1A2B3) és  =
= (A1A2A3,A1A2C3), ahol a síkok közös A1A2 egyenesét az
(A1A2A3,A1A2C3), ahol a síkok közös A1A2 egyenesét az vektor szerint irányítjuk.
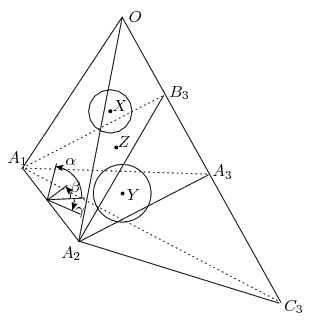
Akalmazzuk a Lemmát az A1A2 egyenesre, az A1A2A3, A1A2B3, A1A2O síkokra és az X pontra; a lemma szerint
| (1) |
Hasonlóan, a Lemmát az A1A2 egyenesre, az A1A2A3, A1A2C3, A1A2B3 síkokra és az Y pontra alkalmazva kapjuk, hogy
| (2) |
Végül, a Lemmát az A1A2 egyenesre, az A1A2A3, A1A2C3, A1A2O síkokra és az Z pontra alkalmazva,
Láthatjuk, hogy dZ 0 esetén a dX,rX,dY,rY,dZ távolságok egyértelműen meghatározzák
0 esetén a dX,rX,dY,rY,dZ távolságok egyértelműen meghatározzák  -t, és ha az 1,2,3 indexeket ciklikusan felcseréljük, ugyanezt az értéket kapjuk. A Z pont tehát ugyanakkora tvolságra van az összes OAi+1Ai2 és CiAi+1Ai2 síktól.
-t, és ha az 1,2,3 indexeket ciklikusan felcseréljük, ugyanezt az értéket kapjuk. A Z pont tehát ugyanakkora tvolságra van az összes OAi+1Ai2 és CiAi+1Ai2 síktól.
Abban az elfajuló esetben, ha valamelyik i-re a CiAi+1Ai+2 és OAi+1Ai+2 síkok szimmetrikusak az A1A2A3 síkra, akkor a C1,C2,C3 pontokat egy kicsit elmozgathatjuk úgy, hogy a gömbök továbbra is létezzenek; az ilyen elrendezések határhelyzeteként megkaphatjuk az eredetit.
Statisztika:
2 dolgozat érkezett. 0 pontot kapott: 2 versenyző.
A KöMaL 2011. novemberi matematika feladatai

