Problem A. 729. (September 2018)

A. 729. In a cyclic quadrilateral \(\displaystyle ABCD\), the diagonals meet at point \(\displaystyle E\), the midpoint of side \(\displaystyle AB\) is \(\displaystyle F\), and the feet of perpendiculars from \(\displaystyle E\) to the lines \(\displaystyle DA\), \(\displaystyle AB\), and \(\displaystyle BC\) are \(\displaystyle P\), \(\displaystyle Q\), and \(\displaystyle R\), respectively. Prove that the points \(\displaystyle P\), \(\displaystyle Q\), \(\displaystyle R\), and \(\displaystyle F\) are concyclic.

Proposed by Máté Weisz, Szeged

(7 pont)

Deadline expired on October 10, 2018.

Solution 1.

Lemma. Let \(\displaystyle A_1A_2\ldots A_n\) and \(\displaystyle B_1B_2\ldots B_n\) be similar polygons with the same orientation. For every \(\displaystyle i\), let \(\displaystyle C_i\) be the midpoint of the line segment \(\displaystyle A_iB_i\). Then either the points \(\displaystyle C_1,C_2,\ldots,C_n\) coincide, or the polygon \(\displaystyle C_1C_2\ldots C_n\) is similar to \(\displaystyle A_1A_2\ldots A_n\) and has the same orientation.

Proof: Place the points on the complex plane. Let \(\displaystyle \varphi\) be the orientation preservin similarity that moves the polygon \(\displaystyle A_1A_2\ldots A_n\) to \(\displaystyle B_1B_2\ldots B_n\). That is, \(\displaystyle \varphi\) is a linear function, \(\displaystyle \varphi(z)=az+b\) with some complex numbers \(\displaystyle a\ne0\) and \(\displaystyle b\). The transformation \(\displaystyle \psi(z)=\frac{z+\varphi(z)}{2}\) maps the points \(\displaystyle A_1,\ldots,A_n\) to \(\displaystyle C_1,\ldots,C_n\), respectively. If \(\displaystyle \psi(z)\) is constant then \(\displaystyle C_1=\ldots=C_n\). Otherwise \(\displaystyle \psi\) is also an orentation preserving similarity.

Proof for the problem statement::

Let \(\displaystyle \sphericalangle DAC = \alpha\). Consider first the case when \(\displaystyle \alpha\) is acute.

Let the reflections of \(\displaystyle E\) about lines \(\displaystyle AD\) and \(\displaystyle BC\) be \(\displaystyle K\) and \(\displaystyle L\), respectively. Then

\(\displaystyle \sphericalangle KAP = \sphericalangle PAE = \sphericalangle DAC = \sphericalangle DBC = \sphericalangle EBR = \sphericalangle REL = \alpha. \)

As can be seen the isosceles triangles \(\displaystyle AEK\) and \(\displaystyle BLE\) are similar and the have the same orientation as the quatrilateral \(\displaystyle ABCD\).

By applying the lemma to these triangles, we conclude that the midpoints of \(\displaystyle AB\), \(\displaystyle KE\) and \(\displaystyle EL\) form another similar triangle, so \(\displaystyle \triangle AEK \sim \triangle BLE \sim \triangle FRP\), and hence

\(\displaystyle \sphericalangle PFR = \sphericalangle KAE = 2\alpha. \)

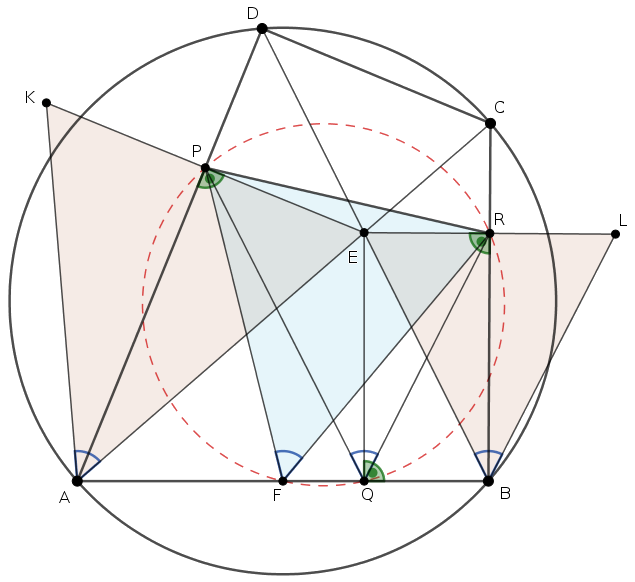
By the right angles at \(\displaystyle P,Q,R\), the quadrilaterals \(\displaystyle AQEP\) and \(\displaystyle BREQ\) are cyclic, so \(\displaystyle \sphericalangle PQE = \sphericalangle PAE = \alpha\) and \(\displaystyle \sphericalangle EQR = \sphericalangle EDP = \alpha\), therefore

\(\displaystyle \sphericalangle PQR = 2\alpha. \)

This shows that \(\displaystyle \sphericalangle PFR =\sphericalangle PQR = 2\alpha\); and porves tha problem statement.

If \(\displaystyle \alpha\) is obtuse then \(\displaystyle 2\alpha>180^\circ\), and the triangles \(\displaystyle AEK\) and \(\displaystyle BLE\) have reversed orientation. The proof can be done in the same way, by replacing \(\displaystyle 2\alpha\) with \(\displaystyle 360^\circ-2\alpha\):

\(\displaystyle PFR\sphericalangle = PQR\sphericalangle = 360^\circ-2\alpha. \)

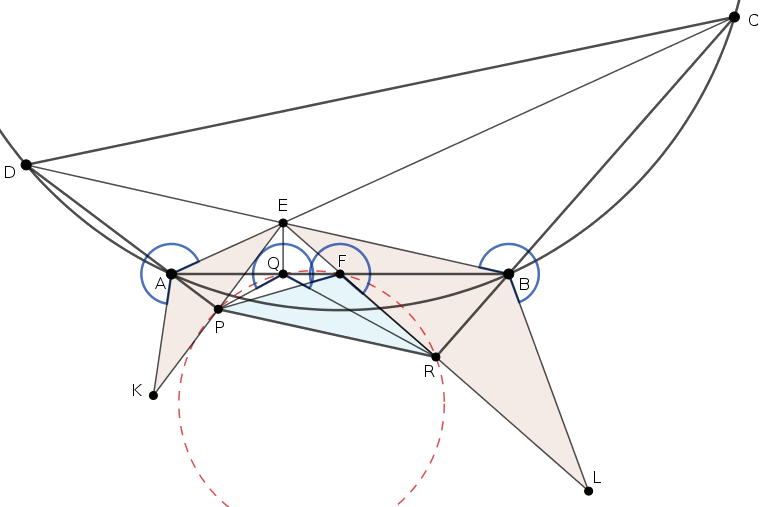
(The case consideration can be avoided if we use oriented angles.)

Finally, if \(\displaystyle \alpha\) is a right angle then \(\displaystyle P=A\) and \(\displaystyle Q=B\); the points \(\displaystyle P,F,Q,R\) are collinear.

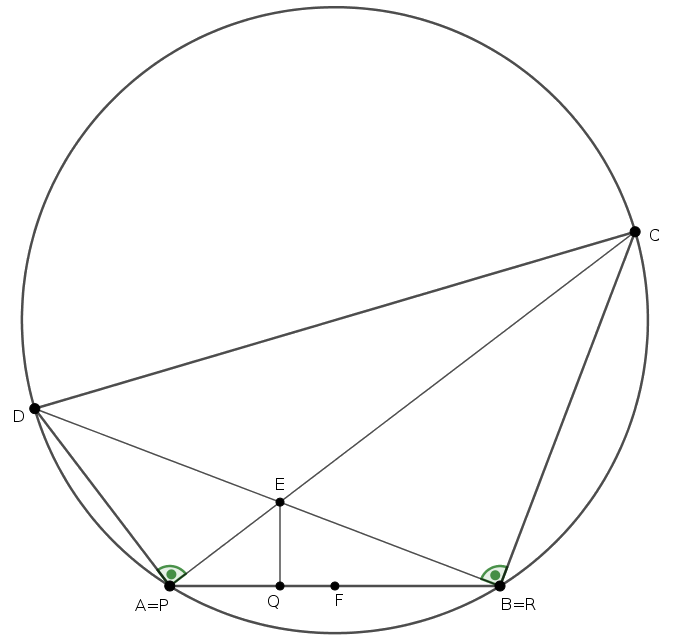
(In this case the statement is inaccurate; the circle \(\displaystyle PQRF\) generates to a line.)

Solution 2. (outline).

Here we present the solution in the case when \(\displaystyle \sphericalangle DAC\) is acute.

In the cyclic quardilaterals \(\displaystyle AQEP\), \(\displaystyle ABCD\) and \(\displaystyle BREQ\) we have \(\displaystyle \sphericalangle PQE = \sphericalangle DAC = \sphericalangle DBC = \sphericalangle EQR\), so \(\displaystyle QE\) bisects \(\displaystyle \sphericalangle PQR\); the line \(\displaystyle AQB\) is the external angle bisectior of \(\displaystyle \sphericalangle PQR\).

In any triangle, an external angle bisector and the perpendicular bisector of the opposite side meet on the circumcircle, so it suffices to proof that in triangle \(\displaystyle PQR\), the point \(\displaystyle F\) lies on the perpendicular bisector of \(\displaystyle PR\), or equivalently, \(\displaystyle FP=FR\).

Let \(\displaystyle P'\) and \(\displaystyle E'\) be the reflections of \(\displaystyle P\) and \(\displaystyle E\) about line \(\displaystyle AQB\). The points \(\displaystyle P',Q,R\) are collienar and \(\displaystyle FP=FP'\), it is enough to proof \(\displaystyle FP'=FR\).

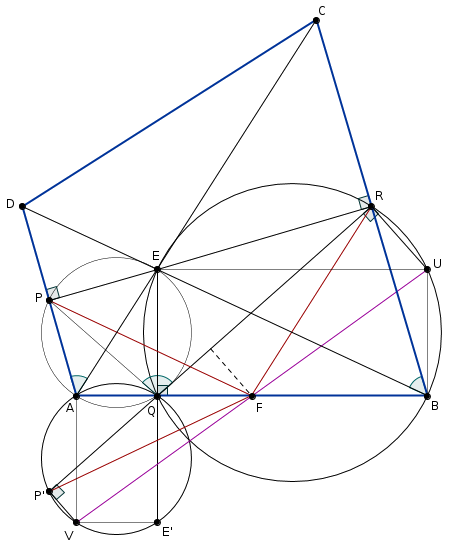
On the circles \(\displaystyle BREQ\) and \(\displaystyle AP'E'Q\), let \(\displaystyle U\) and \(\displaystyle V\) be the points opposite to \(\displaystyle Q\), respectively. We claim that \(\displaystyle F\) is the midpoint of \(\displaystyle UV\). Notice that \(\displaystyle AVE'Q\) and \(\displaystyle BUEQ\) are rectangles, so

\(\displaystyle \overrightarrow{QU}+\overrightarrow{QV} = \big(\overrightarrow{QB}+\overrightarrow{QE}\big)+ \big(\overrightarrow{QA}+\overrightarrow{QE'}\big)= \overrightarrow{QA}+\overrightarrow{QB} = 2\overrightarrow{QF}. \)

That proofs that \(\displaystyle F\) bisects \(\displaystyle UV\).

Now consider the trapezoid \(\displaystyle RP'VU\), that has right abgles at \(\displaystyle R\) and\(\displaystyle P'\). \(\displaystyle F\) is the midpoint of \(\displaystyle UV\), so \(\displaystyle F\) lies on the midline of the trapezoid that is the perpendicluar bisector of \(\displaystyle P'R\). Hence, \(\displaystyle FP'=FR\), done.

Statistics:

12 students sent a solution.
7 points:	Kerekes Anna, Márton Dénes, Milan Haiman, Schrettner Jakab, Shuborno Das, Szabó 417 Dávid, Szabó Kristóf, Weisz Máté.
6 points:	Pituk Gábor.
4 points:	1 student.
Unfair, not evaluated:	1 solutions.
Not shown because of missing birth date or parental permission:	1 solutions.

Problems in Mathematics of KöMaL, September 2018