Az A. 729. feladat (2018. szeptember)

A. 729. Az \(\displaystyle ABCD\) húrnégyszög átlóinak metszéspontja \(\displaystyle E\), az \(\displaystyle AB\) oldal felezőpontja \(\displaystyle F\), és az \(\displaystyle E\) pont merőleges vetületei a \(\displaystyle DA\), \(\displaystyle AB\) és \(\displaystyle BC\) egyeneseken rendre \(\displaystyle P\), \(\displaystyle Q\), illetve \(\displaystyle R\). Igazoljuk, hogy a \(\displaystyle P\), \(\displaystyle Q\), \(\displaystyle R\) és \(\displaystyle F\) pontok egy körre illeszkednek.

Javasolta: Weisz Máté (Szeged)

(7 pont)

A beküldési határidő 2018. október 10-én LEJÁRT.

1. megoldás.

Lemma. Legyenek \(\displaystyle A_1A_2\ldots A_n\) és \(\displaystyle B_1B_2\ldots B_n\) azonos irányítású, hasonló sokszögek. Legyen az \(\displaystyle A_iB_i\) szakasz \(\displaystyle C_i\) pontja olyan, hogy \(\displaystyle \lambda\cdot A_iC_i=B_iC_1\) minden \(\displaystyle 1\le i\le n\) esetén. Ekkor a \(\displaystyle C_1,C_2,\ldots,C_n\) pontok egybeesnek, vagy pedig \(\displaystyle C_1C_2\ldots C_n\) és \(\displaystyle A_1A_2\ldots A_n\) azonos irányítású hasonló sokszögek.

Bizonyítás: A pontokat helyezzük el a komplex számsíkon. Legyen \(\displaystyle \varphi\) az az irányítástartó hasonlósági transzformáció, amely az \(\displaystyle A_1A_2\ldots A_n\) sokszöget az a \(\displaystyle B_1B_2\ldots B_n\) sokszögbe viszi. Minden irányítástartó hasonlóság lineáris függvény, tehát \(\displaystyle \varphi(z)=az+b\) alkalmas \(\displaystyle a\ne0\) és \(\displaystyle b\) komplex számokkal. Az \(\displaystyle A_1,\ldots,A_n\) pontokat a \(\displaystyle \psi(z)=\frac{z+\varphi(z)}{2}\) függvény a \(\displaystyle C_1,\ldots,C_n\) pontokba viszi. Ha \(\displaystyle \psi(z)\) konstans, akkor \(\displaystyle C_1=\ldots=C_n\). Ellenkező esetben \(\displaystyle \psi\) is egy irányitástartó hasonlóság.

A feladat állításának bizonyítása:

Legyen \(\displaystyle DAC\sphericalangle = \alpha\). Először vizsgáljuk azt az esetet, ha \(\displaystyle \alpha\) hegyesszög.

Legyen \(\displaystyle E\) tükörképe az \(\displaystyle AD\) és \(\displaystyle BC\) egyenesekre \(\displaystyle K\), illetve \(\displaystyle L\). Ekkor a tükrözések miatt \(\displaystyle AK=AE\) és \(\displaystyle BL=BE\), továbbá, mivel \(\displaystyle ABCD\) húrnégyszög,

\(\displaystyle KAP \sphericalangle = PAE \sphericalangle = DAC \sphericalangle = DBC \sphericalangle = EBR \sphericalangle = REL \sphericalangle = \alpha. \)

Ebből látjuk, hogy az \(\displaystyle AEK\) és \(\displaystyle BLE\) egyenlő szárú háromszögek hasonlóak és az \(\displaystyle ABCD\) négyszöggel azonos körüljárásúak.

A lemmát erre a két háromszögre alkalmazva kapjuk, hogy az \(\displaystyle AB\), \(\displaystyle KE\) és \(\displaystyle EL\) szakaszok felezőpontjai, azaz \(\displaystyle F\), \(\displaystyle P\) és \(\displaystyle R\) is ezekhez hasonló háromszöget határoz meg. Tehát \(\displaystyle AEK \triangle \sim BLE \triangle \sim FRP \triangle\), és így

\(\displaystyle PFR\sphericalangle = KAE \sphericalangle = 2\alpha. \)

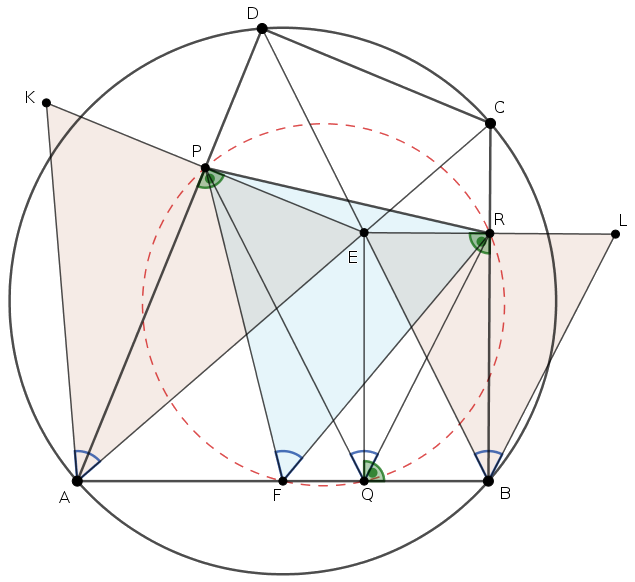
A \(\displaystyle P,Q,R\) pontoknál levő derékszögek miatt \(\displaystyle AQEP\) és \(\displaystyle BREQ\) húrnégyszögek, ezért \(\displaystyle PQE\sphericalangle = PAE \sphericalangle = \alpha\) és \(\displaystyle EQR\sphericalangle = EDP \sphericalangle = \alpha\), tehát

\(\displaystyle PQR\sphericalangle = 2\alpha. \)

Ezzel beláttuk, hogy \(\displaystyle PFR\sphericalangle = PQR\sphericalangle = 2\alpha\); ez bizonyítja az állítást.

Ha \(\displaystyle \alpha\) tompaszög, akkor \(\displaystyle 2\alpha>180^\circ\), ezért az \(\displaystyle AEK\) és \(\displaystyle BLE\) háromszögek irányítása megfordul. A bizonyítás ugyanígy mondható el, csak \(\displaystyle 2\alpha\) helyett mindenhol \(\displaystyle 360^\circ-2\alpha\) szöget kell írni:

\(\displaystyle PFR\sphericalangle = PQR\sphericalangle = 360^\circ-2\alpha. \)

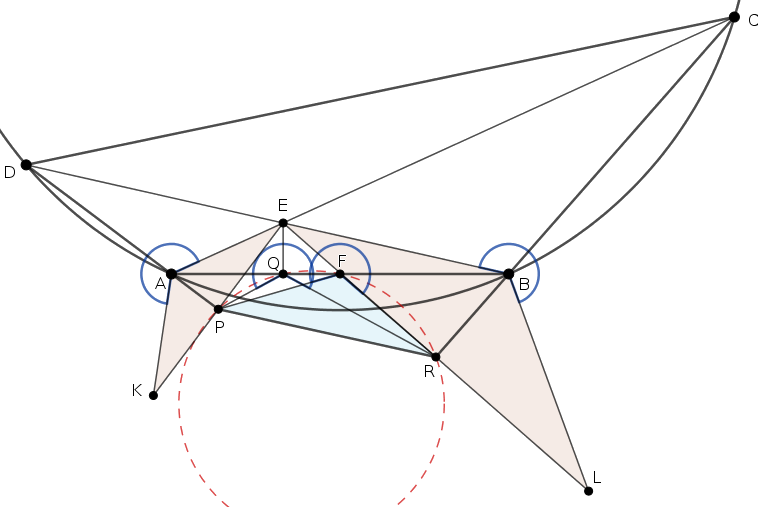
(A geometriai diszkussziót részben elkerülhetjük, ha irányított szögekkel számolunk.)

Végül, ha \(\displaystyle \alpha\) derékszög, akkor \(\displaystyle P=A\) és \(\displaystyle Q=B\); a \(\displaystyle P,F,Q,R\) pontok egy egyenesre esnek.

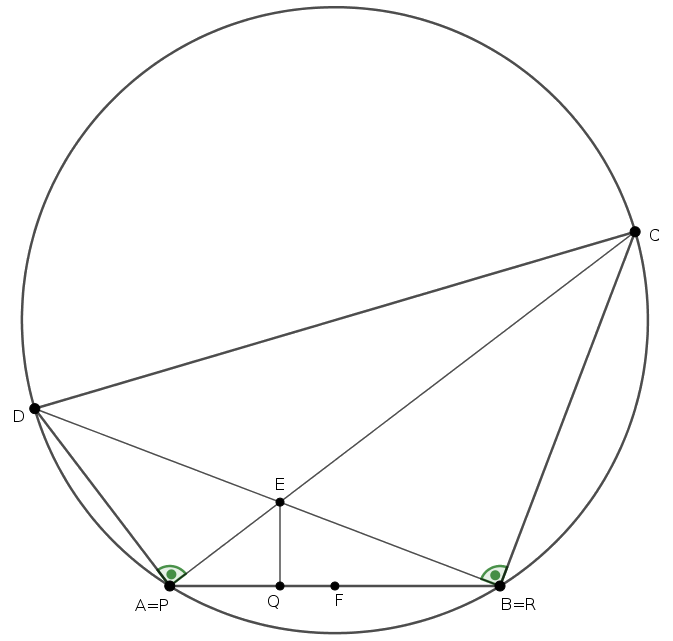
Ebben az esetben az állítás pontatlan; a \(\displaystyle PQRF\) kör egyenessé fajulhat.

2. megoldás (vázlat). ("Szögfelezőre tükrözni kell.")

Most csak abban az esetben mutatjuk be a megoldást, ha \(\displaystyle DAC\angle\) hegyesszög. A teljes megoldáshoz az első megoldáshoz geometriai diszkusszió is szükséges.

Az \(\displaystyle AQEP\), \(\displaystyle ABCD\) és \(\displaystyle BREQ\) húrnégyszögekben \(\displaystyle PQE\sphericalangle = DAC\sphericalangle = DBC\sphericalangle = EQR\sphericalangle\), így a \(\displaystyle QE\) egyenes felezi a \(\displaystyle PQR\sphericalangle\) szöget; a rá merőleges \(\displaystyle AQB\) egyenes a \(\displaystyle PQR\sphericalangle\) külső szögfelezője. Bármely háromszögben a külső szögfelező és a szemközti oldal merőleges felezője a körülírt körön metszi egymást; ezt a \(\displaystyle PQR\) háromszögre alkalmazva, a feladat állítása következne abból, hogy \(\displaystyle F\) a \(\displaystyle PR\) szakasz felező merőlegesén van, azaz \(\displaystyle FP=FR\).

Legyen \(\displaystyle P'\) és \(\displaystyle E'\) a \(\displaystyle P\) és \(\displaystyle E\) tükörképe az \(\displaystyle AQB\) egyenesre. Ekkor \(\displaystyle P',Q,R\) egy egyenesen van, és \(\displaystyle FP=FP'\), és elég azt igazolnunk, hogy \(\displaystyle FP'=FR\).

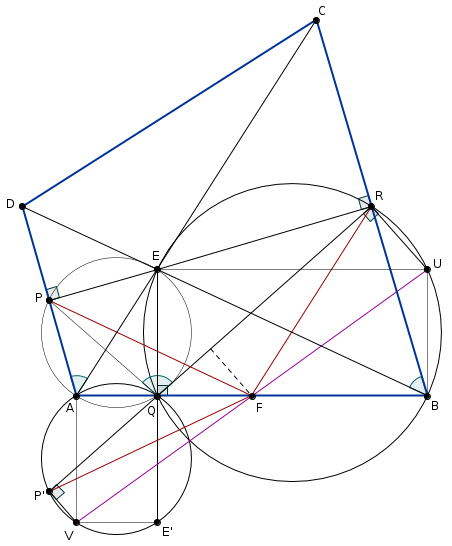
Az \(\displaystyle BREQ\) és \(\displaystyle AP'E'Q\) a körökön legyen \(\displaystyle U\), illetve \(\displaystyle V\) a \(\displaystyle Q\)-val szemközti pont. Azt állítjuk, hogy \(\displaystyle F\) az \(\displaystyle UV\) szakasz felezőpontja. Vegyük észre, hogy \(\displaystyle AVE'Q\) és \(\displaystyle BUEQ\) is téglalap, mert az \(\displaystyle A,B,Q,E,E'\) csúcsoknál derékszögeik vannak, így

\(\displaystyle \overrightarrow{QU}+\overrightarrow{QV} = \big(\overrightarrow{QB}+\overrightarrow{QE}\big)+ \big(\overrightarrow{QA}+\overrightarrow{QE'}\big)= \overrightarrow{QA}+\overrightarrow{QB} = 2\overrightarrow{QF}. \)

Ez pedig éppen azt jelenti, hogy \(\displaystyle F\) az \(\displaystyle UV\) szakasz felezőpontja.

Most tekintsük az \(\displaystyle RP'VU\) négyszöget. Ez egy derékszögű trapéz, mert \(\displaystyle R\)-nél és \(\displaystyle P'\)-nél derékszöge van. Az \(\displaystyle F\) az \(\displaystyle UV\) szár felezőpontja; ebből következik, hogy \(\displaystyle F\) rajta van a trapéz középvonalán, ami az alapokra merőleges \(\displaystyle P'R\) szár felező merőlegese. Tehát \(\displaystyle FP'=FR\), kész.

Statisztika:

12 dolgozat érkezett.
7 pontot kapott:	Kerekes Anna, Márton Dénes, Milan Haiman, Schrettner Jakab, Shuborno Das, Szabó 417 Dávid, Szabó Kristóf, Weisz Máté.
6 pontot kapott:	Pituk Gábor.
4 pontot kapott:	1 versenyző.
Nem versenyszerű:	1 dolgozat.
Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt:	1 dolgozat.

A KöMaL 2018. szeptemberi matematika feladatai