 |
Az A. 771. feladat (2020. február) |
A. 771. Legyen az \(\displaystyle ABC\) háromszög beírt köre \(\displaystyle \omega\), mely a \(\displaystyle BC\) oldalt a \(\displaystyle D\) pontban érinti. Az \(\displaystyle AD\) egyenes második metszéspontja az \(\displaystyle \omega\) körrel legyen \(\displaystyle G\). Az \(\displaystyle \omega\) körhöz a \(\displaystyle G\) pontban húzott érintő messe az \(\displaystyle AB\) és \(\displaystyle AC\) oldalakat rendre az \(\displaystyle E\) és az \(\displaystyle F\) pontban. A \(\displaystyle DEF\) körülírt körének \(\displaystyle D\)-től különböző metszéspontja \(\displaystyle \omega\)-val legyen \(\displaystyle M\). A \(\displaystyle BCG\) körülírt körének a \(\displaystyle G\)-től különböző metszéspontja \(\displaystyle \omega\)-val legyen \(\displaystyle N\). Bizonyítandó, hogy az \(\displaystyle AD\) és \(\displaystyle MN\) egyenesek párhuzamosak.
Javasolta: Győrffy Ágoston (Remeteszőlős)
(7 pont)
A beküldési határidő 2020. március 10-én LEJÁRT.
Megoldásvázlat. I. Vizsgáljuk először azt az esetet, ha \(\displaystyle AB\ne AC\).
Legyen \(\displaystyle H\) az \(\displaystyle BC\) és \(\displaystyle EF\) egyenesek metszéspontja. A \(\displaystyle BDCFGE\) hatszögre feírt a Brianchon-tételból következik, hogy az \(\displaystyle BF\), \(\displaystyle CE\) és \(\displaystyle ADG\) egyenesek egy ponton menek át, emiatt a \(\displaystyle (HD,BC)\) és \(\displaystyle (HG,EF)\) pontnégyesek harmonikusak.
Legyen \(\displaystyle k_1\) a \(\displaystyle HG\) átmérőjű kör, ekkor \(\displaystyle E,F\) egymás inverze \(\displaystyle k_1\)-re. A beírt kör és az \(\displaystyle EFD\) kör is szimmetrikus \(\displaystyle k_1\)-re; ezért metszéspontjaik, \(\displaystyle D\) és \(\displaystyle M\) egymás inverzei. Ugyanígy, \(\displaystyle G\) és \(\displaystyle N\) egymás inverze a \(\displaystyle HD\) átmérőjű \(\displaystyle k_2\) körre.
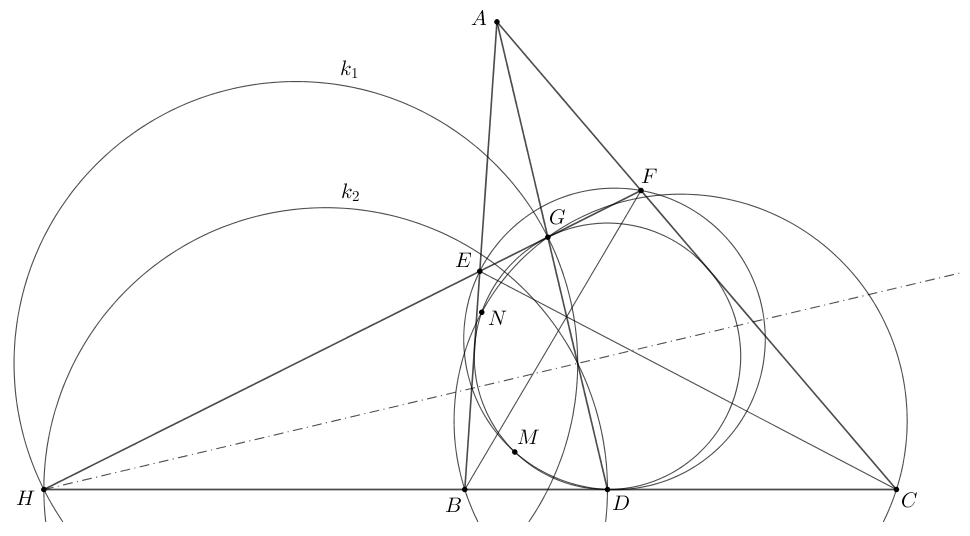
Ezek után a \(\displaystyle DHG\) szög felezőjére szimmetrikus \(\displaystyle D\) és \(\displaystyle G\), \(\displaystyle k_1\) és \(\displaystyle k_2\), tehát \(\displaystyle M\) és \(\displaystyle N\) is. Ezzel igazoltuk, hogy \(\displaystyle DG\) és \(\displaystyle MN\) is merőleges a \(\displaystyle DHG\) szög felezőjére, tehát párhuzamosak egymással.
II. Ha \(\displaystyle AB=AC\), akkor az ábra szimmetrikus az \(\displaystyle ADG\) egyenesre, \(\displaystyle M=D\) és \(\displaystyle N=G\), és az állítás triviális.
Statisztika:
6 dolgozat érkezett. 7 pontot kapott: Bán-Szabó Áron, Beke Csongor, Csaplár Viktor, Várkonyi Zsombor, Weisz Máté. 5 pontot kapott: 1 versenyző.
A KöMaL 2020. februári matematika feladatai
