Az A. 840. feladat (2022. december)

A. 840. Az \(\displaystyle ABC\) háromszög beírt köre az oldalakat az \(\displaystyle X\), \(\displaystyle Y\) és \(\displaystyle Z\) pontban érinti. Az \(\displaystyle XYZ\) háromszögben az \(\displaystyle X\) és az \(\displaystyle Y\) csúcsból induló magasságok talppontjai \(\displaystyle X'\) és \(\displaystyle Y'\). Az \(\displaystyle X'Y'\) egyenes az \(\displaystyle ABC\) háromszög körülírt körét a \(\displaystyle P\) és a \(\displaystyle Q\) pontban metszi. Bizonyítandó, hogy \(\displaystyle X\), \(\displaystyle Y\), \(\displaystyle P\) és \(\displaystyle Q\) egy körre esnek.

Javasolta: Simon László (Budapest)

(7 pont)

A beküldési határidő 2023. január 10-én LEJÁRT.

Legyen \(\displaystyle XY\) és \(\displaystyle X'Y'\) metszéspontja \(\displaystyle D\). Mivel \(\displaystyle X\), \(\displaystyle Y\), \(\displaystyle X'\) és \(\displaystyle Y'\) egy körre esnek (\(\displaystyle XY\) Thálesz-körére), ezért \(\displaystyle DX\cdot DY=DX'\cdot DY'\). Ez azt jelenti, hogy a \(\displaystyle D\) pont hatványa ugyanakkora az \(\displaystyle XYZ\) háromszög körülírt körére és Feuerbach-körére nézve, azaz rajta van a két kör hatványvonalán. Most megmutatjuk, hogy ezzel a két körrel koaxiális az eredeti háromszög körülírt köre is (azaz mindhárom körnek ugyanaz a hatványvonala). Ezzel készen leszünk, mert a \(\displaystyle D\) pont hatványa az \(\displaystyle ABC\) körülírt körére \(\displaystyle DP\cdot DQ\), és így \(\displaystyle DX\cdot DY=DP\cdot DQ\), vagyis \(\displaystyle X\), \(\displaystyle Y\), \(\displaystyle P\) és \(\displaystyle Q\) egy körre esnek.

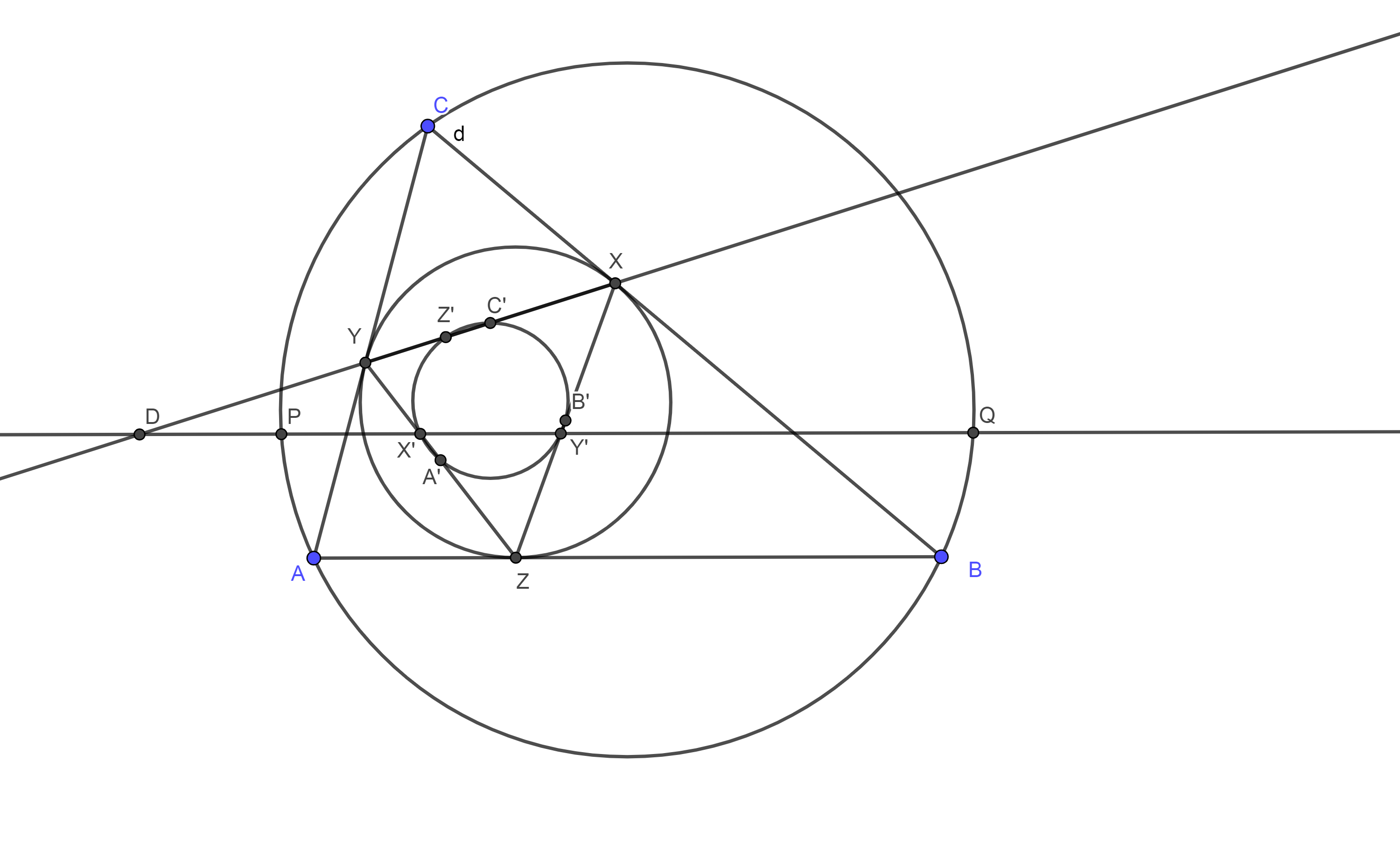
Ehhez először belátjuk, hogy az \(\displaystyle XYZ\) háromszög Feuerbach köre az \(\displaystyle ABC\) háromszög körülírt körének inverz képe az \(\displaystyle XYZ\) háromszög körülírt körére nézve. Ez kijön abból a jól ismert állításból, hogy egy külső pont inverz képe megegyezik a pontból húzott érintők érintési pontjai által alkotott szakasz felezőpontjával, azaz pl. az \(\displaystyle A\) pont inverz képe az \(\displaystyle YZ\) szakasz felezőpontja, ami rajta van az \(\displaystyle XYZ\) háromszög Feuerbach-körén, és hasonló igaz \(\displaystyle B\) és \(\displaystyle C\) inverz képére is.

Végül azt kell megmutatnunk, hogy az inverzió alapköre és két kör, melyek egymás inverz képei, koaxiálisak (legyenek a körök \(\displaystyle k\), \(\displaystyle l\) és \(\displaystyle l'\)). Ez nyilvánvaló, ha a körök metszik az inverzió alapkörét, de esetünkben sajnos közös pont nélküli körökről van szó. Megjegyezzük, hogy mivel a három kör középpontjai egy egyenesre esnek, ezért elég egyetlen pontot találni, melynek mindhárom körre nézve ugyanakkora a hatványa.

Általános esetben a következő módon járhatunk el: vegyünk egy tetszőleges kört (ez lesz \(\displaystyle \gamma\)), amely merőleges \(\displaystyle k\)-ra és \(\displaystyle l\)-re (ezeket a köröket megkapjuk, ha \(\displaystyle k\) és \(\displaystyle l\) hatványvonalán választunk egy pontot a körökön kívül, ez lesz \(\displaystyle \gamma\) középpontja, és onnan érintőket húzunk \(\displaystyle k\)-hoz és \(\displaystyle l\)-hez, \(\displaystyle \gamma\) sugarát pedig a középpont és az érintési pontok távolságának választjuk). Mivel \(\displaystyle \gamma\) merőleges az inverzió alapkörére, ezért a képe az inverziónál saját maga (ez az inverzió jól ismert tulajdonsága), így \(\displaystyle l\) képe az inverziónál \(\displaystyle l'\), és az inverzió szögtartó, így \(\displaystyle \gamma\) az \(\displaystyle l'\) körre is merőleges lesz. Ekkor viszont \(\displaystyle \gamma\) középpontjának egyforma mindhárom körre vonatkozó hatványa (a sugarának a négyzete), és ebből következik az állítás.

Statisztika:

20 dolgozat érkezett.
7 pontot kapott:	Diaconescu Tashi, Foris Dávid, Lovas Márton, Molnár-Szabó Vilmos, Móricz Benjámin, Németh Márton, Seres-Szabó Márton, Sida Li, Simon László Bence, Sztranyák Gabriella, Tarján Bernát, Varga Boldizsár, Virág Rudolf, Wiener Anna.
6 pontot kapott:	Chrobák Gergő.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2022. decemberi matematika feladatai