Az A. 851. feladat (2023. április)

A. 851. Legyenek $\displaystyle k$, $\displaystyle l$ és $\displaystyle m$ pozitív egész számok. Legyen $\displaystyle ABCDEF$ egy olyan középpontosan szimmetrikus hatszög, melynek szögei mind $\displaystyle 120^{\circ}$-osak, oldalainak hosszai pedig $\displaystyle AB=k$, $\displaystyle BC=l$ és $\displaystyle CD=m$. Jelölje $\displaystyle f(k,l,m)$ azt, hogy hányféle módon lehet az $\displaystyle ABCDEF$ hatszöget átfedés nélkül lefedni olyan egységoldalú rombuszokkal, melyek egyik szöge $\displaystyle 120^{\circ}$.

Bizonyítsuk be, hogy rögzített $\displaystyle l$ és $\displaystyle m$ mellett létezik olyan $\displaystyle g_{l,m}$ polinom, melyre minden pozitív egész $\displaystyle k$ esetén $\displaystyle f(k,l,m)=g_{l,m}(k)$, és állapítsuk meg $\displaystyle g_{l,m}$ fokát $\displaystyle l$ és $\displaystyle m$ függvényében.

Javasolta: Gyenes Zoltán (Budapest)

(7 pont)

A beküldési határidő 2023. május 10-én LEJÁRT.

Tegyük fel, hogy ki van parkettázva valahogy a hatszög, és tekintsük a két szemközti, $\displaystyle k$ hosszú oldalt. Látható, hogy van $\displaystyle k$ darab út az egyik oldalról a másikra úgy, hogy a rombuszok azon középvonalain haladunk végig, melyek két olyan szemközti felezőpontot kötnek össze, amik párhuzamosak a $\displaystyle k$ hosszú oldallal. Ezek az utak nem keresztezhetik egymást, így minden ilyen út éppen $\displaystyle l$-szer lép az egyik, és $\displaystyle m$-szer a másik irányba. Tekintsünk úgy a hatszögre, hogy a $\displaystyle k$ hosszú oldal vízsintes, és nevezzük az utakon a kétféle irányú lépéseket jobb (J) és bal (B) lépéseknek, ahol mindig $\displaystyle l$ darab J lépés van. Ekkor az, hogy nem metszik egymást éppen azt jelenti, hogy ha tekintünk egy utat, akkor minden $\displaystyle t$-re az első $\displaystyle t$ lépésben ez az út legfeljebb annyiszor léphet jobbra, mint a tőle jobbra lévő út. Azaz ha egy $\displaystyle k$ soros és $\displaystyle l+m$ oszlopos táblázat soraiba egymás alá beírjuk a J-B sorozatokat, amik leírják az utakat, akkor tetszőleges két sorra és $\displaystyle t$ számra igaznak kell lennie, hogy a lentebbi sorban legalább annyi J van az első $\displaystyle t$ helyen, mint a fentebbiben. Megfordítva, könnyen látható, hogy egy ilyen táblázathoz olyan utak tartoznak, amik nem metszik egymást, és ilyen utak egyértelműen meghatároznak egy romboszukkal parkettázást. Így a feladat ekvivalens azzal, hogy az ilyen táblázatok számáról bizonyítsuk be, hogy polinom $\displaystyle k$-ban.

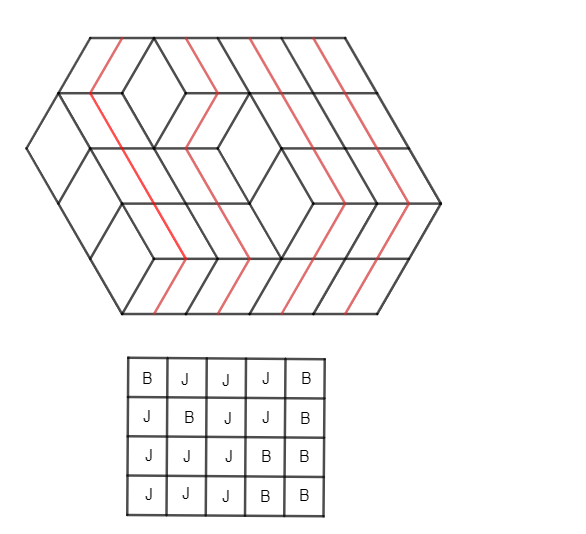
Tekintsük azokat a $\displaystyle l+m$ hosszú J-B sorozatokat, melyekben pontosan $\displaystyle l$ darab J van. Definiáljunk ezeken egy részbenrendezést, egy sorozat akkor kisebb, mint egy másik, ha a táblázatban kerülhet fölé (azaz tetszőleges kezdőszeletben legfeljebb annyi J van, mint a másikban). Világos, hogy ez a tulajdonság tranzitív. Legyen $\displaystyle P$ az így kapott részbenrendezett halmaz. Ekkor a megfelelő táblázatokat le tudjuk számolni a következőképpen: Vegyünk egy tetszőleges nem üres $\displaystyle L$ láncot $\displaystyle P$-ből, tegyük fel, hogy $\displaystyle s_L$ elemből áll. Ekkor azon táblázatok, amikben pontosan ezek a sorok szerepelnek éppen $\displaystyle \binom{k-1}{s_L-1}$, mivel a részbenrendezés megadja, hogy milyen sorrendben következnek a sorok, így csak azt dönthetjük el, hogy melyikből hány legyen, így $\displaystyle s_L-1$ elválasztó vonalat kell behúznunk a $\displaystyle k$ sor közé. A feltétel szerint láncnak kell lennie azon J-B sorozatok halmazának $\displaystyle P$-ben, amik egy táblázatban szerepelnek, így az összes $\displaystyle P$-beli $\displaystyle L$ láncra összegezve a fenti $\displaystyle \binom{k-1}{s_L-1}$ kifejezést éppen a keresett mennyiséget kapjuk.

Mivel $\displaystyle l$ és $\displaystyle m$ fix, így rögzített mennyiségű $\displaystyle \binom{k-1}{s_L-1}$ alakú tagot adunk össze, amik $\displaystyle k$-ban $\displaystyle s_L-1$ fokú polinomok. Így $\displaystyle f(k,l,m)$ valóban polinom $\displaystyle k$-ban, melynek foka a leghosszabb lánc hossza $\displaystyle P$-ben mínusz 1. Minden sorozathoz rendeljük hozzá, hogy hány (J,B) pár van, melyre a J megelőzi a B-t. Ez az $\displaystyle m$ darab B-vel kezdődő sorozatra 0, és az $\displaystyle m$ darab B-re végződő sorozatra $\displaystyle lm$, minden más sorozatra ezek közé esik. Látható, hogy ha egy sorozat $\displaystyle P$-ben nagyobb, mint egy másik, akkor ez a hozzárendelt érték is nagyobb, így egy lánc hossz legfeljebb $\displaystyle lm+1$ lehet. Ez pedig tényleg el is érhető, például ha kiindulunk az $\displaystyle m$ darab B-vel kezdődő sorozatból, majd a jobb oldali B-t egyesével a végére toljuk, utána a következő B-t, és így tovább, míg el nem jutunk addig, hogy minden B a sorozat végén van. Tehát $\displaystyle lm+1$ a leghosszabb lánc hossza $\displaystyle P$-ben, így $\displaystyle f(k,l,m)$ egy $\displaystyle lm$ fokú polinom $\displaystyle k$-ban.

Statisztika:

5 dolgozat érkezett.
7 pontot kapott:	Sida Li, Varga Boldizsár.
5 pontot kapott:	1 versenyző.
2 pontot kapott:	1 versenyző.
0 pontot kapott:	1 versenyző.

A KöMaL 2023. áprilisi matematika feladatai