 |
Az A. 857. feladat (2023. szeptember) |
A. 857. Adott az \(\displaystyle ABC\) hegyesszögű háromszög, melynek leghosszabb oldala \(\displaystyle BC\). Legyen a háromszög magasságpontja \(\displaystyle H\), a \(\displaystyle B\) és \(\displaystyle C\) csúcsaiból induló magasságok talppontjai rendre \(\displaystyle D\) és \(\displaystyle E\), továbbá az \(\displaystyle AB\) és \(\displaystyle AC\) oldalak felezőpontjai rendre \(\displaystyle F\) és \(\displaystyle G\). A \(\displaystyle DF\) és \(\displaystyle EG\) egyenesek egymást az \(\displaystyle X\) pontban metszik. Legyen az \(\displaystyle EFX\), illetve \(\displaystyle DGX\) háromszögek köréírt köreinek középpontja rendre \(\displaystyle O_1\) és \(\displaystyle O_2\), az \(\displaystyle O_1O_2\) szakasz felezőpontja pedig \(\displaystyle M\). Igazoljuk, hogy \(\displaystyle X\), \(\displaystyle H\), \(\displaystyle M\) egy egyenesre esnek.
Javasolta: Varga Boldizsár (Verőce)
(7 pont)
A beküldési határidő 2023. október 10-én LEJÁRT.
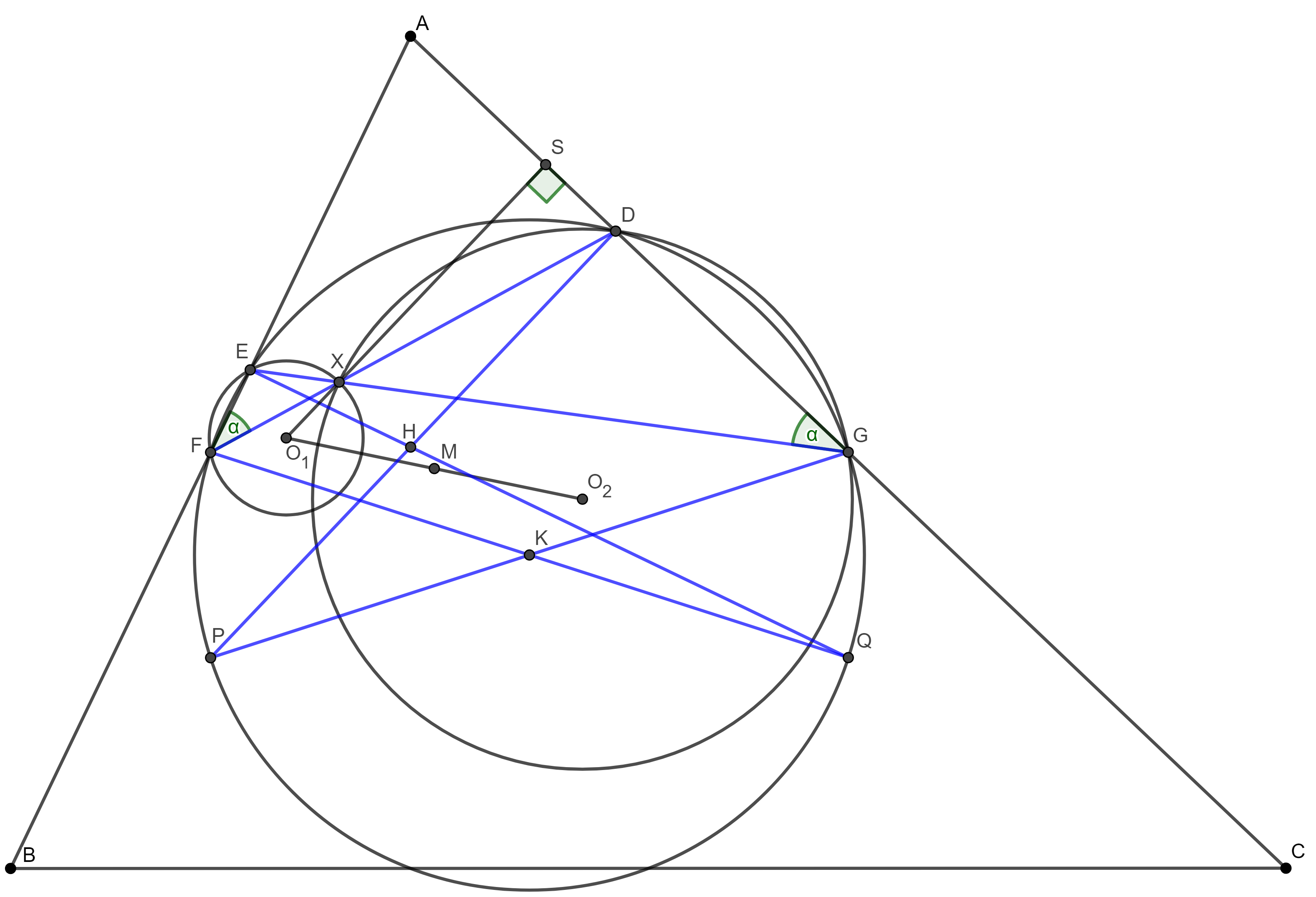
Megmutatjuk, hogy mindhárom pont illeszkedik az \(\displaystyle ABC\) háromszög Euler-egyenesére. \(\displaystyle H\)-ról ez ismert, ezért elegendő \(\displaystyle M\)-re és \(\displaystyle X\)-re bizonyítanunk.
Jelölje az \(\displaystyle ABC\) háromszög Feuerbach-körének középpontját \(\displaystyle K\). Ismert, hogy \(\displaystyle K\) is rajta van az \(\displaystyle ABC\) háromszög Euler-egyenesén. Legyen a Feuerbach-kör második metszéspontja a \(\displaystyle BD\) és \(\displaystyle CE\) szakaszokkal rendre \(\displaystyle P\) és \(\displaystyle Q.\) Ismert, hogy \(\displaystyle D,\) \(\displaystyle E,\) \(\displaystyle F,\) illetve \(\displaystyle G\) a Feuerbach-körön vannak. Mivel \(\displaystyle FEQ\sphericalangle=90^{\circ}\), így Thalesz-tételből következik, hogy \(\displaystyle Q\) az \(\displaystyle F\)-fel átellenes pont, illetve analóg módon \(\displaystyle P\) a \(\displaystyle G\)-vel átellenes pont a Feuerbach-körön, azaz az \(\displaystyle FQ\) és \(\displaystyle GP\) egyenesek áthaladnak \(\displaystyle K\)-n. Felírva a Pascal-tételt a Feuerbach-körbe írt \(\displaystyle EQFDPG\) hatszögre, kapjuk, hogy \(\displaystyle EQ\cap{DP}=H,\) \(\displaystyle QF\cap{PG}=K,\) illetve \(\displaystyle FD\cap{GE}=X\) egy egyenesre esnek, azaz \(\displaystyle X\) is rajta van az \(\displaystyle ABC\) háromszög Euler-egyenesén.
Most azt fogjuk belátni, hogy \(\displaystyle M\) éppen az \(\displaystyle XK\) szakasz felezőpontja, világos, hogy ezzel kész lennénk. Ehhez azt mutatjuk meg, hogy az \(\displaystyle XO_1KO_2\) négyszög paralelogramma, sőt szemközti oldalpárjai nemcsak hogy párhuzamosak, de merőlegesek az \(\displaystyle AC,\) illetve \(\displaystyle AB\) egyenesekre. A szimmetria miatt elegendő ezt csak az \(\displaystyle O_2K,\) illetve \(\displaystyle O_1X\) egyenesekről megmutatnunk. Az \(\displaystyle O_2K\) egyenesre ez világos, hiszen \(\displaystyle O_2\) és \(\displaystyle K\) is rajta vannak a \(\displaystyle DG\) szakasz felezőmerőlegesén. Legyen \(\displaystyle S\) az \(\displaystyle O_1X\) egyenes és \(\displaystyle AC\) metszéspontja, továbbá legyen \(\displaystyle DGE \sphericalangle = \alpha\). Ekkor az \(\displaystyle DFE \sphericalangle=\alpha\), mivel \(\displaystyle GDEF\) húrnégyszög. Az \(\displaystyle XEF\) körből \(\displaystyle XO_1E \sphericalangle=2\alpha\), mivel középponti szög, amiből \(\displaystyle EXO_1 \sphericalangle=90^{\circ}-\alpha\). Ekkor \(\displaystyle GXS \sphericalangle=90^{\circ}-\alpha\) is teljesül, mivel csúcsszög, amiből kapjuk, hogy \(\displaystyle XSG \sphericalangle\) tényleg derékszög, ahogy akartuk. Ezzel a bizonyítáat befejeztük.
Statisztika:
25 dolgozat érkezett. 7 pontot kapott: Anay Aggarwal, Bencz Benedek, Bodor Mátyás, Chrobák Gergő, Czanik Pál, Diaconescu Tashi, Duchon Márton, Farkas 005 Bendegúz, Fleischman Illés, Foris Dávid, Forrai Boldizsár, Gömze Norken, Hodossy Réka, Kovács Benedek Noel, Lincoln Liu, Selim Cadîr, Simon László Bence, Tarján Bernát, Varga Boldizsár, Virág Lénárd Dániel, Virág Rudolf, Wiener Anna. 6 pontot kapott: Philip Stefanov. 4 pontot kapott: 1 versenyző. 3 pontot kapott: 1 versenyző.
A KöMaL 2023. szeptemberi matematika feladatai
