 |
Az A. 875. feladat (2024. március) |
A. 875. \(\displaystyle a)\) Két játékos egy kooperatív játékot játszik. A játék előtt megbeszélhetnek egy stratégiát, de a kezdés után nem beszélhetnek, és nem tudnak egymásról semmit. A játékvezető minden kör előtt szabadon dönt, hogy abban a körben melyik játékos következzen. Egy körben a soron lévő játékos megtippelheti, hogy hányadik kör van. A játékos tudja, hogy ez hányadik kör, amikor őt választotta a játékvezető, de semmit nem tud arról, hogy a másik játékos hányszor került sorra. Ha helyes a tipp, akkor kapnak egy pontot. A játékosok arról sem kapnak visszajelzést, hogy szereztek-e pontot. A játékosok akkor nyernek, ha összegyűjtöttek 100 pontot. Létezik-e olyan stratégia, amellyel biztosan nyernek véges sok körön belül?
\(\displaystyle b)\) Mi a helyzet akkor, ha a többi feltételt nem változtatva a játékosok a körükben kettőt is tippelhetnek, és ha valamelyik tippük helyes, akkor kapnak egy pontot?
Javasolta: Szűcs Gábor, (Budapest)
(7 pont)
A beküldési határidő 2024. április 10-én LEJÁRT.
a) Legyen a két játékos \(\displaystyle A\) és \(\displaystyle B\). Egy pont mindig elérhető, például ha mindkét játékos minden körben \(\displaystyle 1\)-et tippel. Ennél több azonban nem biztos: Jelölje \(\displaystyle A\) játékos tippjét saját maga \(\displaystyle k.\) kihívásakor \(\displaystyle a_k\), valamint legyen hasonlóan definiálva a \(\displaystyle b_k\) sorozat \(\displaystyle B\) tippjeire.
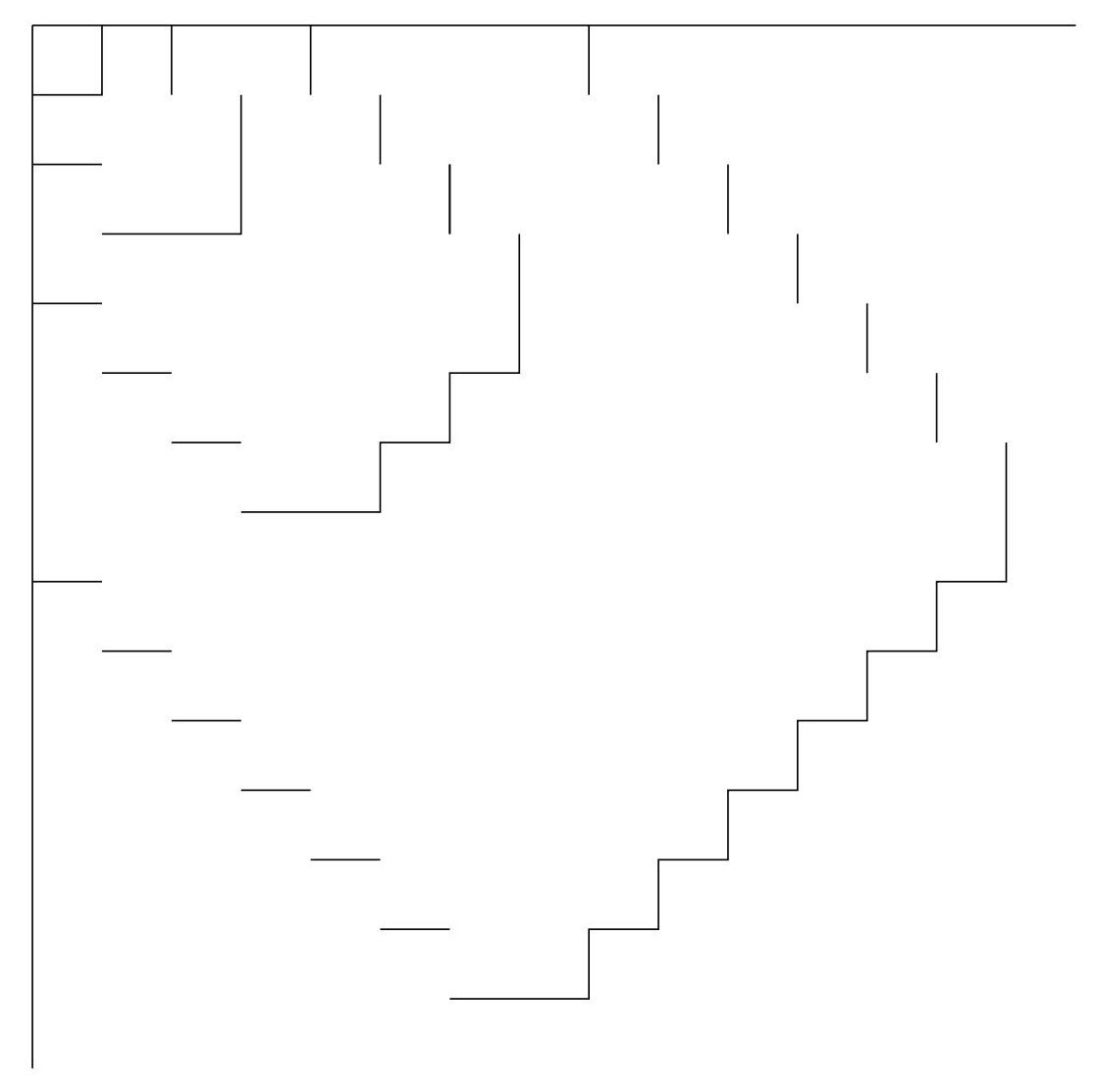
A játék menetét a 4. síknegyed egységnégyzeteiből álló táblázatban fogjuk szemléltetni a következő módon: A bal felső (\(\displaystyle (0,0)\) indexű négyzet) sarokból indulunk és amennyiben az adott körben az \(\displaystyle A\) játékost hívják ki, akkor jobbra lépünk egyet a táblázatban, ellenkező esetben lefele. Továbbá helyezzünk el függőleges, illetve vízszintes falakat a táblázatban, előbbieket a \(\displaystyle (k-1,-(a_k-k))\) koordinátájú négyzetek jobb szélső oldalán, míg utóbbiakat a \(\displaystyle (-(b_k-k),k-1)\) koordinátájú négyzetek alsó oldalán. Gondoljuk meg, hogy ekkor a játék arra fogalmazható át, hogy kezdetben, a játékosok minden függőleges oszlop jobb szélére, és vízszintes sor alsó szélére legfeljebb egy falat elhelyezhetnek. Ezek után ebben a táblázatban minden lépésben lépünk egyet jobbra vagy lefelé (ezt a játékvezető dönti el), és ha áthaladunk egy vízszintes vagy függőleges falon, akkor a játékosok kapnak egy pontot. Ugyanis ha a játékvezető eddig \(\displaystyle n\)-szer szólította \(\displaystyle A\)-t, és \(\displaystyle m\)-szer \(\displaystyle B\)-t, és most \(\displaystyle A\)-t szólítja, akkor a játékosok akkor kapnak pontot, ha \(\displaystyle a_{n+1}=n+m+1\), ami a táblázatban éppen annak felel meg, hogy az \(\displaystyle (n,-m)\) mezőről az \(\displaystyle (n+1,-m)\) mezőre lépünk, így éppen akkor haladunk át falon, ha \(\displaystyle -(a_{n+1}-(n+1))=-m\), ami átrendezve az \(\displaystyle a_{n+1}=n+m+1\) egyenlettel ekvivalens. A játékosok célja az, hogy úgy húzzanak be falakat, hogy akárhogyan lépked jobbra és lefelé a játékvezető, mindenképpen legalább 100 falba ütközzön véges sok lépésen belül.
Tegyük fel, hogy a játékosok valahogyan behúztak falakat a szabályoknak megfelelő módon. Játszon a játékvezető a következőképpen. Amíg a játékosoknak nincs pontja, mindig lépjen tetszőlegesen úgy, hogy ha lehetséges, nem ad pontot a játékosoknak a lépésével. Az első pontjukat a játékosok csak úgy tudják megszerezni, ha olyan négyzetbe jutunk, melynek az alsó és jobb oldala is fal. Lépjen ekkor jobbra a játékvezető. Ezek után lépjen addig jobbra, amíg el nem érünk egy falat. Ha ez sosem történik meg, akkor világos, hogy a játékosok nem szereznek több pontot. Ha egy falhoz érünk, akkor mivel korábban (amikor pontot szereztek a játékosok) ezen négyzet sorának alsó szélén már volt fal, most lefele lépéssel biztosan nem kapnak pontot a játékosok. Ezek után lefele haladjunk addig, amíg falhoz nem érünk. Itt megint igaz lesz az, hogy a mező oszlopának jobb szélén már volt fal, így tudunk jobbra menni. És így tovább, mindig haladjunk felváltva jobbra vagy lefele ütközésig, és így sosem tudnak a játékosok több, mint egy pontot szerezni.
b) Készítsük el az előzőhöz hasonló táblázatot. Ekkor annyi különbség lesz az a) feladatrészhez képest, hogy most minden sor alsó szélén és oszlop jobb oldali szélén két fal is szerepelhet. Ebben az esetben már tudnak nyerni a játékosok az alábbi konstrukcióval (a végtelenségig folytatjuk a minta alapján). A játékvezető kénytelen minden rétegen metszeni egy falat, vagyis biztosan szereznek 100 pontot véges sok lépésen belül a játékosok.
Statisztika:
15 dolgozat érkezett. 7 pontot kapott: Hodossy Réka, Holló Martin, Szakács Ábel, Tianyue DAI, Varga Boldizsár, Vödrös Dániel László, Wiener Anna. 6 pontot kapott: Foris Dávid. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző. Nem számítjuk a versenybe a születési dátum vagy a szülői nyilatkozat hiánya miatt: 1 dolgozat.
A KöMaL 2024. márciusi matematika feladatai

