Problem A. 894. (December 2024)

A. 894. In convex polyhedron \(\displaystyle ABCDE\) line segment \(\displaystyle DE\) intersects the plane of triangle \(\displaystyle ABC\) inside the triangle. Rotate the point \(\displaystyle D\) outward into the plane of triangle \(\displaystyle ABC\) around the lines \(\displaystyle AB\), \(\displaystyle BC\), \(\displaystyle CA\); let the resulting points be \(\displaystyle D_1\), \(\displaystyle D_2\), and \(\displaystyle D_3\). Similarly, rotate the point \(\displaystyle E\) outward into the plane of triangle \(\displaystyle ABC\) around the lines \(\displaystyle AB\), \(\displaystyle BC\), \(\displaystyle CA\); let the resulting points be \(\displaystyle E_1\), \(\displaystyle E_2\), and \(\displaystyle E_3\). Show that if the polyhedron has an inscribed sphere, then the circumcircles of \(\displaystyle D_1D_2D_3\) and \(\displaystyle E_1E_2E_3\) are concentric.

Proposed by: Géza Kós, Budapest

(7 pont)

Deadline expired on January 10, 2025.

Solution. The key to the solution is following statement:

Lemma: Let \(\displaystyle ABCD\) be a tetrahedron, and let \(\displaystyle G\) be an arbitrary sphere tangent to the interior of triangles \(\displaystyle ABD\), \(\displaystyle BCD\) and \(\displaystyle ACD\) at points \(\displaystyle T_1\), \(\displaystyle T_2\) and \(\displaystyle T_3\). Let point \(\displaystyle T_1'\) be obtained by rotating point \(\displaystyle T_1\) outward around \(\displaystyle AB\) into plane \(\displaystyle ABC\), \(\displaystyle T_2'\) and \(\displaystyle T_3'\) is defined similarly; points \(\displaystyle D_1\), \(\displaystyle D_2\) and \(\displaystyle D_3\) are defined as in the problem. Then the circumcircles of \(\displaystyle T_1'T_2'T_3'\) and \(\displaystyle D_1D_2D_3\) are concentric.

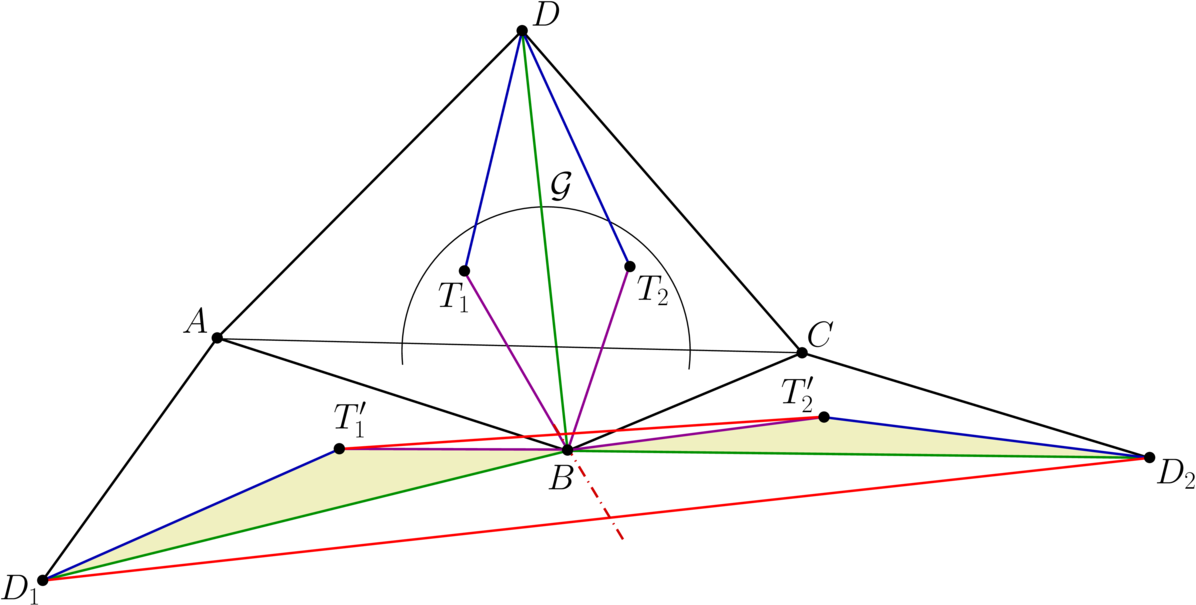
To prove the statement it is enough to show that the perpendicular bisectors of \(\displaystyle T_1'T_2'\) and \(\displaystyle D_1D_2\) coincide. Now note that \(\displaystyle BT_1=BT_2\), since these are tangents from point \(\displaystyle B\) to sphere \(\displaystyle G\). Similarly \(\displaystyle DT_1=DT_2\). This implies that triangles \(\displaystyle \triangle BT_1D\) and \(\displaystyle \triangle BT_2D\) are congruent to each other. Since \(\displaystyle \triangle BT_1'D_1\) is a rotation of \(\displaystyle \triangle BT_1D\) around \(\displaystyle AB\), and \(\displaystyle \triangle BT_2'D_2\) is a rotation of \(\displaystyle BT_2D\) around \(\displaystyle BC\), therefore \(\displaystyle \triangle BT_1'D_1\) and \(\displaystyle \triangle BT_2'D_2\) are also congruent to each other. It's also easy to check that these triangles have opposite orientations, therefore there is a line reflection (with an axis through their common vertex \(\displaystyle B\)), thus quadrilateral \(\displaystyle T_1'T_2'D_2D_1\) is a symmetric trapezoid with bases \(\displaystyle T_1'T_2'\) and \(\displaystyle D_1D_2\), which proves the statement.

Now to prove the statement in the problem, let's choose \(\displaystyle G\) as the inscribed sphere of \(\displaystyle ABCDE\), and let \(\displaystyle U_1\), \(\displaystyle U_2\) and \(\displaystyle U_3\) denote the points where \(\displaystyle G\) is tangent to the interiors of angles \(\displaystyle \angle AEB\), \(\displaystyle \angle BEC\) and \(\displaystyle \angle CEA\) (\(\displaystyle T_1\), \(\displaystyle T_2\) and \(\displaystyle T_3\) are defined as above). Let \(\displaystyle U_1'\), \(\displaystyle U_2'\) and \(\displaystyle U_3'\) be defined as the appropriate rotations of \(\displaystyle U_1\), \(\displaystyle U_2\) and \(\displaystyle U_3\) into plane \(\displaystyle ABC\). Now according to the lemma, the circumcirlces \(\displaystyle E_1E_2E_3\) and \(\displaystyle U_1'U_2'U_3'\) are concentric. Now the remaining thing to discover is this: \(\displaystyle T_i'=U_i'\). Let's prove this for \(\displaystyle T_1'\) and \(\displaystyle U_1\)': \(\displaystyle AT_1=AU_1\) since these are both tangents from \(\displaystyle A\) to \(\displaystyle G\); similarly \(\displaystyle BT_1=BU_1\). Thus triangles \(\displaystyle \triangle AT_1B\) and \(\displaystyle \triangle AU_1B\) are congruent, and so are their rotations \(\displaystyle AT_1'B\) and \(\displaystyle AU_1'B\). Since \(\displaystyle T_1\) and \(\displaystyle U_1\) are inside triangles \(\displaystyle ABD\) and \(\displaystyle ABE\), respectively, and both these triangles were rotated outward, we prove our claim. This clearly finishes the proof, since triangles \(\displaystyle T_1'T_2'T_3'\) and \(\displaystyle U_1'U_2'U_3'\) are coincide, and consequently also their circumcircles are the same, and we have finished our proof.

Statistics:

12 students sent a solution.
7 points:	Aravin Peter, Bodor Mátyás, Forrai Boldizsár, Gyenes Károly, Holló Martin, Keresztély Zsófia, Szakács Ábel, Varga Boldizsár, Vödrös Dániel László, Xiaoyi Mo.
4 points:	1 student.
0 point:	1 student.

Problems in Mathematics of KöMaL, December 2024