 |
A B. 3837. feladat (2005. szeptember) |
B. 3837. Jelölje P, illetve Q az ABC háromszög AB oldalára kifelé rajzolt ABDE négyzet és a BC oldalára kifelé rajzolt BCGH négyzet középpontját. Az AC és a DH szakaszok felezőpontja R, illetve S. Mutassuk meg, hogy a P, Q, R és S pontok egy négyzet csúcsai.
(4 pont)
A beküldési határidő 2005. október 17-én LEJÁRT.
Megoldás.
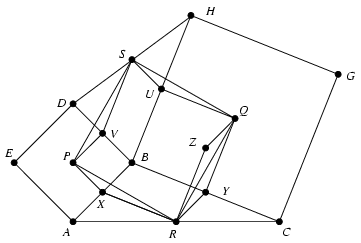
Legyenek X,Y,U és V rendre az AB,BC,BH és BD szakaszok felezőpontjai, Z pedig az Y pontnak a QR szakasz felezőpontjára vonatkozó tükörképe. Mivel az SU szakasz a BDH háromszög középvonala, SU párhuzamos és egyenlő hosszú a VB szakasszal, és így a PX szakasszal is. Hasonlóképpen az UQ és XR szakaszok is párhuzamosak és egyenlő hosszúak. Ezért az UQS - esetleg elfajuló - háromszög eltolással származtatható az XRP háromszögből, amiért is a PRQS négyszög paralelogramma. QZ párhuzamos és egyenlő hosszú az YR szakasszal, ezért BX-szel is, vagyis a PX szakaszból 90o-os elforgatással keletkezik. ZR pedig párhuzamos és egyenlő hosszú a QY szakasszal, amely viszont az XR-rel párhuzamos és egyenlő hosszú BY szakaszból keletkezik ugyancsak 90o-os elforgatással. Következésképpen a QZR háromszög a PXR háromszögből kapható meg 90o-os elforgatással, vagyis a QR szakasz merőleges a PR szakaszra, és hosszuk megegyezik. Ebből már következik, hogy a PRQS paralelogramma négyzet.
Statisztika:
216 dolgozat érkezett. 4 pontot kapott: 159 versenyző. 3 pontot kapott: 24 versenyző. 2 pontot kapott: 14 versenyző. 1 pontot kapott: 6 versenyző. 0 pontot kapott: 13 versenyző.
A KöMaL 2005. szeptemberi matematika feladatai
