A B. 3898. feladat (2006. március)

B. 3898. Ismert, hogy egy tetszőleges tetraéder szemközti éleinek felezőpontjait összekötő szakaszok egy ponton mennek át. Ki lehet-e választani egy tetraéder minden élének egy harmadolópontját úgy, hogy a szemközti élekről választott harmadolópontokat összekötő szakaszok egy ponton menjenek át?

(3 pont)

A beküldési határidő 2006. április 18-án LEJÁRT.

Megoldás:

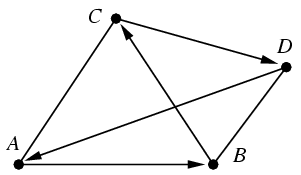
A tetraéder két szemközti élét elhagyva, a megmaradt négy él által alkotott zárt töröttvonalon irányítsuk meg körbe az éleket az ábra szerint. Ha egy irányított élről az első harmadolópontot választottuk, akkor ahhoz rendeljünk egyet, ha a másodikat, akkor pedig kettőt. Ha az ábrán látható irányí tott körön végighaladva egy vagy három alkalommal szerepel az osztópontok mellett 1, akkor a négy pont nincs egy síkban, a hozzájuk tartozó két összekötő szakasz tehát nem metszheti egymást. Vagyis a két szakasz csak akkor mehet át egy ponton, ha az irányított körön végighaladva a számok összege páros. Ha egy él irányát megváltoztatjuk, az összeg paritása is megváltozik.

Tegyük fel, hogy a harmadolópontokat úgy választottuk meg, hogy az összekötő szakaszok egy ponton mennek át. Az e élen lévő számot f(e)-vel jelölve tehát p=f(AB)+f(BC)+f(CD)+f(AD) páros szám. Irányítsuk meg a fennmaradó két élet B-től D felé, illetve A-tól C felé. Az ABDC körön végighaladva két élen haladunk az irányítással ellentétes irányba, vagyis q=f(AB)+f(BD)+f(CD)+f(AC) is páros szám. Az ACBD körön viszont csak egyszer haladunk az irányítással ellentétes irányba, tehát r=f(AC)+f(BC)+f(BD)+f(AD) páratlan.

Ekkor p+q+r egyrészt páratlan, másrészt pedig páros, hiszen benne minden f(e) összeadandó pontosan kétszer szerepel. Ez az ellentmondás mutatja, hogy az osztópontokat nem lehet a kívánt módon kiválasztani.

Statisztika:

23 dolgozat érkezett.
3 pontot kapott:	Anda Roland, Balambér Dávid, Bartha Zsolt, Beck Zoltán, Blázsik Zoltán, Csaba Ákos, Cserép Máté, Duba Zsombor, Elekes Csaba, Herber Máté, Kristóf Panna, Nagy 235 János, Nagy-Baló András, Németh Kitti Noémi, Salát Zsófia, Sümegi Károly, Tolner Ferenc, Tomon István, Vajsz Tibor.
2 pontot kapott:	Pap Bálint, Szabó Levente.
0 pontot kapott:	2 versenyző.

A KöMaL 2006. márciusi matematika feladatai