A B. 3912. feladat (2006. május)

B. 3912. Igazoljuk, hogy minden konvex négyszögnek van olyan csúcsa, amelynek a vele szomszédos két csúcs által meghatározott szakasz felezőpontjára vonatkozó tükörképe nincs a négyszögön kívül.

(4 pont)

A beküldési határidő 2006. június 15-én LEJÁRT.

Megoldás: Legyenek a négyszög csúcsai sorban A,B,C,D, a megfelelő szögek pedig rendre $\alpha$ , $\beta$ , $\gamma$ , $\delta$ . Mivel a négy szög összege 360^o, $\alpha$ + $\beta$ és $\gamma$ + $\delta$ közül az egyik legalább 180^o. Ugyanígy $\beta$ + $\gamma$ és $\delta$ + $\alpha$ közül is az egyik legalább 180^o. Az általánosság megszorítása nélkül feltehetjük, hogy

$\alpha$ + $\beta$ $\ge$ 180^o, $\beta$ + $\gamma$ $\ge$ 180^o.

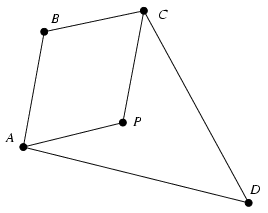
Tekintsük az ABCP paralelogrammát. Ekkor a P pont benne van mind a BAD, mind pedig a BCD zárt szögtartományban, vagyis a P pont vagy az ABCD négyszög belsejébe, vagy annak határára esik. Ez a P pont pedig éppen B-nek az AC szakasz felezőpontjára vonatkozó tükörképe.

Statisztika:

48 dolgozat érkezett.

4 pontot kapott: Almási 270 Gábor András, Árvay Anna, Balambér Dávid, Balog 272 Éva, Csató László, Cseh Ágnes, Czövek Petra, Dombi Soma, Farkas Ádám László, Godó Zita, Győrffy Lajos, Horváth 385 Vanda, Károlyi Márton, Kiss Blanka, Kovács 111 Péter, Kovács 129 Péter, Kristóf Panna, Kunovszki Péter, Kurgyis Eszter, Kutas Péter, Mercz Béla, Mészáros Gábor, Milotai Zoltán, Müller Márk, Nagy 235 János, Nagy-Baló András, Németh 007 Zsolt, Páldy Sándor, Pásztor Attila, Peregi Tamás, Pesti Veronika, Pirkó Dániel, Priksz Ildikó, Schäfer Fanni, Sommer Dániel, Sümegi Károly, Szakács Nóra, Szalkai Balázs, Szalóki Dávid, Szilágyi 987 Csaba, Szirmai Péter, Szudi László, Ta Phuong Linh, Tarlós 103 Gréta, Tomon István, Tossenberger Anna, Tóth 222 Barnabás, Wolosz János.

A KöMaL 2006. májusi matematika feladatai

Már regisztráltál?
Új vendég vagy?