A B. 3934. feladat (2006. október)

B. 3934. Egy derékszögű háromszögbe az ábra szerint egy téglalapot és két négyzetet írtunk. Mutassuk meg, hogy a téglalap magassága a négyzetek magasságának az összege.

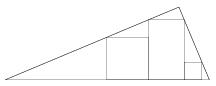
(3 pont)

A beküldési határidő 2006. november 15-én LEJÁRT.

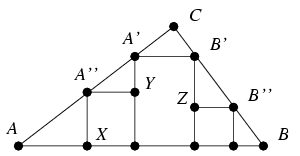
Megoldás. Az ábrán látható derékszögű háromszögek egymáshoz hasonlóak. A párhuzamos szelők tétele miatt AA'/BB'=AC/BC, ugyanígy aránylanak tehát egymáshoz a kis négyzetek odalai: A''X/ZB''=AC/BC, és az A'A''Y háromszög befogói is: A''Y/A'Y=AC/BC. Ezért A''X=A''Y miatt A'Y=ZB'', ahonnan a téglalap magassága A''X+A'Y=A''X+ZB'', amint azt bizonyítani akartuk.

Statisztika:

257 dolgozat érkezett.
3 pontot kapott:	239 versenyző.
2 pontot kapott:	12 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	2 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2006. októberi matematika feladatai