Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

A B. 3939. feladat (2006. október)

B. 3939. Mekkora szög alatt látszik egy 2 egységnyi kerületű derékszögű háromszög átfogója a derékszög belső szögfelezőjének félegyenesén a csúcstól \sqrt{2} távolságra lévő pontból?

(4 pont)

A beküldési határidő 2006. november 15-én LEJÁRT.

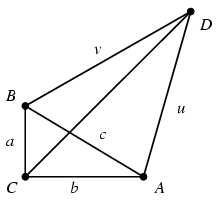
Megoldás. Az ábra jelöléseit használva a+b+c=2 és a2+b2=c2, ahonnan a2+b2=(2-a-b)2, vagyis ab=2a+2b-2. Az ACD, illetve BCD háromszögekre a koszinusz-tételt felírva kapjuk, hogy

u2=b2-2b+2,  v2=a2-2a+2.

Ezért

u2v2=a2b2-2a2b-2ab2+4ab-4a-4b+4+2a2+2b2=

=a2b2-2ab(a+b)+4ab-2ab+2c2=ab(ab-2a-2b+2)+2c2=2c2,

ahonnan az ADB szög koszinuszára

\frac{u^2+v^2-c^2}{2uv}=\frac{4-2a-2b}{2uv}=\frac{c}{uv}=\frac{1}{\sqrt{2}}

adódik. A háromszög átfogója tehát 45o-os szög alatt látszik a D pontból.

Statisztika:

139 dolgozat érkezett.
4 pontot kapott:104 versenyző.
3 pontot kapott:14 versenyző.
2 pontot kapott:4 versenyző.
1 pontot kapott:12 versenyző.
0 pontot kapott:5 versenyző.

A KöMaL 2006. októberi matematika feladatai