A B. 4023. feladat (2007. október)

B. 4023. Egy háromszög egyik oldalán adott egy pont. Szerkesszünk ezen át két olyan egyenest, amelyek a háromszög területét harmadolják.

(3 pont)

A beküldési határidő 2007. november 15-én LEJÁRT.

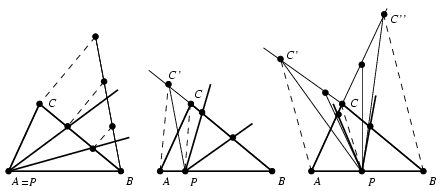
Megoldás: Ha az adott P pont az egyik csúcsba esik, akkor azt a szemközti oldal harmadolópontjaival kell összekötni, melyeket a párhuzamos szelők tételére támaszkodó ismert szerkesztési eljárással kapunk meg. Tegyük fel most, hogy P az ABC háromszög AB oldalának A-hoz közelebbi belső pontja. Ha ez épp az AB oldal H harmadolópontja, akkor nyilván C-vel, illetve a BC odal felezőpontjával kell azt összekötnünk.

Ha P az AH szakasz belső pontja, akkor húzzuk meg azt az egyenest, amely párhuzamos PC-vel és áthalad A-n. Ennek az egyenesnek a BC egyenessel alkotott metszéspontja legyen C'. Az ABC háromszög területe ugyanakkora, mint a PBC' háromszögé. Az előző módszerrel ez utóbbit a P csúcsán áthaladó két egyenessel harmadolhatjuk. Mivel C'B:CB=AB:PB>2/3, a C'B oldal minkét harmadolópontja a BC szakaszra esik, tehát az eredeti feladat megoldását is megkaptuk egyben.

Végül, ha P nem esik az AH szakaszra, akkor az előző módszerrel csak az egyik egyenest kapjuk meg, hiszen a BC' szakasznak csak a B-hez közelebbi harmadolópontja esik a BC oldalra. A másik egyenest most nyilván úgy kapjuk, hogy a PC-vel B-n át húzott párhuzamos AC-vel alkotott metszéspontját A-val összekötő szakasz A-hoz közelebbi harmadolópontját kötjük össze P-vel.

Statisztika:

172 dolgozat érkezett.
3 pontot kapott:	82 versenyző.
2 pontot kapott:	64 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	19 versenyző.
Nem versenyszerű:	2 dolgozat.

A KöMaL 2007. októberi matematika feladatai