A B. 4080. feladat (2008. március)

B. 4080. A körvonalon egymástól függetlenül véletlenszerűen kiválasztunk 3 pontot. Mi annak a valószínűsége, hogy az általuk meghatározott háromszög hegyesszögű?

(4 pont)

A beküldési határidő 2008. április 15-én LEJÁRT.

Megoldás: Tegyük fel egyszerűség kedvéért, hogy a kör kerülete egységnyi, és legyen A a körvonal egy rögzített pontja. Szimmetria okok miatt a keresett valószínűség megegyezik annak a valószínűségével, hogy ha egymástól függetlenűl egy B és egy C pontot kiválasztunk a körvonalon, akkor a kör O középpontja az ABC háromszög belsejébe esik. Ha az A,B pontok O-ra vonatkozó tükörképét A',B' jelöli, akkor ez azzal ekvivalens, hogy BA,A' és C a (rövidebbik) A'B' ív belső pontja.

Rögzítve egy körüljárási irányt, egy-egy értelmű megfeleltetést létesíthetünk az összes (B,C) pontpárok és a [0,1)×[0,1) egységnégyzet (b,c) pontjai között, ahol egy X pontra x jelöli az irányított AX ív hosszát. Azon feltételnek, mely szerint az ABC háromszög hegyesszögű, megfelelő (b,c) pontok halmazát az ábrán besatírozott rész szemlélteti, a határpontokat figyelmen kívül hagyva.

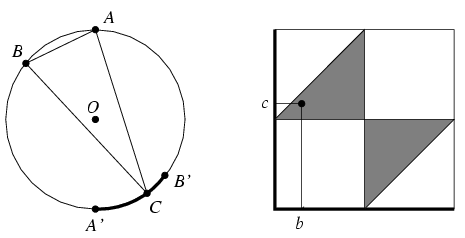
Mivel annak valószínűsége, hogy a P pont egy adott XY ívre esik, megegyezik az XY ív hosszával, a B,C pontok független választása miatt úgy érvelhetünk, hogy a keresett valószínűség megegyezik a besatírozott tartomány területével, ami 1/4-del egyenlő.

Statisztika:

89 dolgozat érkezett.
4 pontot kapott:	72 versenyző.
3 pontot kapott:	7 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	4 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2008. márciusi matematika feladatai