A B. 4103. feladat (2008. szeptember)

B. 4103. Adott ABCD téglalap BC és CD oldalán szerkesszük meg a P és Q pontokat úgy, hogy ABPQ olyan deltoidot alkosson, amely szimmetrikus az AP átlóra.

(3 pont)

A beküldési határidő 2008. október 15-én LEJÁRT.

Megoldás: Legyen AB=CD=a, BC=DA=b. A feltétel miatt AQ=AB=a, vagyis a Q pontot úgy kapjuk, hogy a CD szakaszt elmetsszük az A középpontú a sugarú körvonallal, a P pont pedig a BAQ szög felezőjének a BC szakasszal alkotott metszéspontja kell legyen. Ha a szerkesztés elvégezhető, akkor így valóban a feladat megoldását kapjuk.

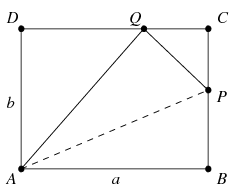
Megmutatjuk, hogy ez pontosan akkor lehetséges, ha ab, mely esetben a megoldás egyértelmű lesz. Ha a<b, akkor a fenti körvonal egyáltalán nem metszi a CD egyenest, tehát nincsen megoldás. Ha a=b, akkor az eljárásból Q=D, P=C adódik. Tegyük fel végül, hogy a>b. A körvonal a DC egyenest két pontban metszi, melyek közül pontosan egy esik a CD szakaszra, ez lesz tehát a Q pont. Ellenőrizzük, hogy QC<CB. Valóban, b<a miatt 2b²<2ab, a²-2ab+b²<a²-b², , vagyis

Ha egy elképzelt P pontot a CB oldalon C-ből B-be mozgatunk, akkor a QP távolság szigorúan monoton nő, PB pedig csökken, vagyis pontosan egy olyan helyzet lesz, amikor PQ=PB, ez kell legyen az a pont, amelyet a fenti szerkesztési eljárás szolgáltat.

Statisztika:

273 dolgozat érkezett.
3 pontot kapott:	141 versenyző.
2 pontot kapott:	117 versenyző.
1 pontot kapott:	10 versenyző.
0 pontot kapott:	5 versenyző.

A KöMaL 2008. szeptemberi matematika feladatai