A B. 4108. feladat (2008. szeptember)

B. 4108. Egy háromszög szögfelezői a háromszög köré írt kört a P, Q, R pontokban metszik. Szerkesszük meg P, Q, R ismeretében a háromszöget.

(4 pont)

A beküldési határidő 2008. október 15-én LEJÁRT.

Megoldás: Képzeljük el a háromszöget megszerkesztettnek. A háromszög A,B,C csúcsai és a P,Q,R pontok a háromszög köré írt kört hat ívre osztják fel az ábrán látható módon. A háromszög szögeit a szokásos módon jelölve a kerületi és középponti szögek közötti összegfüggés alapján mindegyik ívre meghatározhatjuk, hogy a kör O középpontjából mekkora szög alatt látszik.

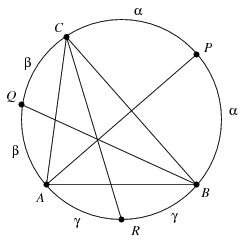
Mivel a PQ,QR,RP ívek mindegyike 180^o-nál kisebb szög alatt látszik, a feladatnak csak akkor lehet megoldása, ha a P,Q,R pontok egy hegyesszögű háromszöget határoznak meg. Megmutatjuk, hogy ez esetben a feladatnak pontosan egy megoldása van. Vegyük észre, hogy ha az +/2+/2 nagyságú QAR szögből kivonjuk a /2+/2 nagyságú RPQ szöget, akkor éppen az szöget kapjuk. Mivel a QAR és RPQ szögek egymást 180^o-ra egészítik ki, az szöget úgy kaphatjuk meg, hogy az egyenesszögből kivonjuk az RPQ szög kétszeresét (más szóval az ROQ szöget), ez pedig a C csúcs helyzetét egyértelműen meghatározza. Kell még látnunk, hogy az így kapott C pont a PQ ívre esik, vagy ami ezzel egyenértékű, hogy

Ez viszont azonnal következik abból, hogy a PQR háromszög hegyesszögű.

A leírtak alapján tehát az A,B,C pontokat a következő módon szerkeszthetjük meg. Először megszerkesztjük a PQR háromszög köré írható k kört és annak O középpontját. Ezek után az OP félegyenesre, mint szögszárra, a PQR forgásiránnyal megegyező módon felmérjük az ROQ szög kiegészítő szögét. Ezen szög másik szára metszi ki a k körből a C csúcsot. Ugyanezt az eljárást a P,Q,R pontok megfelelő ciklikus permutációja esetén is elvégezve az A és B csúcsokat is egyértelműen megszerkeszthetjük, és egyszerűen meggondolható, hogy így valóban a feladat megoldását kapjuk.

Statisztika:

166 dolgozat érkezett.
4 pontot kapott:	Ágoston Tamás, Bányi Máté, Bencskó György Árpád, Blázsik Zoltán, Cséke Balázs, Deák Zsolt, Éles András, Fonyó Dávid, Frankl Nóra, Huszár Kristóf, Kószó Simon, Kovács 235 Gábor, Kovács 888 Adrienn, Lovas Lia Izabella, Márkus Bence, Mészáros András, Pósfai Balázs, Roberts Vivienne, Somogyi Ákos, Székely Eszter, Varga 171 László, Weisz Ágoston, Weisz Gellért, Zsakó András.
3 pontot kapott:	101 versenyző.
2 pontot kapott:	13 versenyző.
1 pontot kapott:	12 versenyző.
0 pontot kapott:	16 versenyző.

A KöMaL 2008. szeptemberi matematika feladatai