 |
A B. 4194. feladat (2009. szeptember) |
B. 4194. Egy háromszög C csúcsánál levő szöge derékszög. A C-hez tartozó szögfelező és magasság a köré írt kört a D, illetve az E pontban metszi. A háromszög nem rövidebbik befogója b. Igazoljuk, hogy a CDE töröttvonal hossza .
(4 pont)
A beküldési határidő 2009. október 12-én LEJÁRT.
Megoldás. Legyen a körülírt kör átmérője egységnyi, a \(\displaystyle b\) befogó melleti szög pedig \(\displaystyle \alpha\le 45^\circ\). Mivel az átfogó éppen a kör átmérője, \(\displaystyle b=\cos\alpha\).
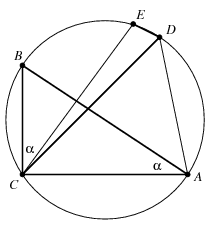
Az ábra jelöléseit használva, a \(\displaystyle BCD\) és a \(\displaystyle BAD\) szög egyaránt \(\displaystyle 45^\circ\)-os, vagyis a \(\displaystyle CD\) húr az \(\displaystyle A\) pontból \(\displaystyle 45^\circ+\alpha\), az \(\displaystyle ED\) húr pedig a \(\displaystyle C\) pontból \(\displaystyle 45^\circ-\alpha\) szög alatt látszik. Ezért valóban
\(\displaystyle CD+DE=\sin(45^\circ+\alpha)+\sin(45^\circ-\alpha)=2\sin45^\circ\cos\alpha= \sqrt{2}\cos\alpha=b\sqrt{2}.\)
Statisztika:
138 dolgozat érkezett. 4 pontot kapott: 127 versenyző. 3 pontot kapott: 7 versenyző. 2 pontot kapott: 1 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2009. szeptemberi matematika feladatai
