 |
A B. 4198. feladat (2009. szeptember) |
B. 4198. Egy szabályos tetraéder alaplapján megrajzoljuk a középvonalakat. Minden középvonal felezőpontját összekötjük a középvonallal párhuzamos oldallap csúcspontjaival. Hányadrésze az így kapott három tetraéder közös részének térfogata a tetraéder térfogatának?
(4 pont)
A beküldési határidő 2009. október 12-én LEJÁRT.
Megoldás. Fogjuk fel a három tetraédert egy-egy olyan gúlának, melyek alaplapja a tetraéder alaplapjának síkjába esik, azzal szemközti csúcsuk pedig egybeesik a tetraéder alaplappal szemközti \(\displaystyle O\) csúcsával. A három alaplap az \(\displaystyle ABF\), a \(\displaystyle BCD\), illetve a \(\displaystyle CAE\) háromszög, melyek közös része a \(\displaystyle DGEHFI\) hatszög. A három tetraéder közös része tehát a \(\displaystyle DGEHFI\) hatszög alapú \(\displaystyle O\) csúcsú gúla, melynek térfogata úgy aránylik az eredeti tetraéder térfogatához, mint a \(\displaystyle DGEHFI\) alaplap területe az \(\displaystyle ABC\) háromszög területéhez; ez utóbbit jelölje \(\displaystyle t\).
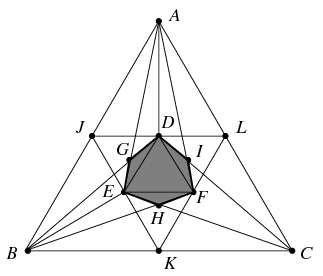
Az \(\displaystyle AJL\), \(\displaystyle BKJ\), \(\displaystyle CLK\) és \(\displaystyle JKL\) szabályos háromszögek területe \(\displaystyle t/4\), az \(\displaystyle ADJ\) és \(\displaystyle BEJ\) háromszögeké \(\displaystyle t/8\), a \(\displaystyle DEF\) és \(\displaystyle DEJ\) háromszögeké pedig \(\displaystyle t/16\). Az \(\displaystyle ABED\) szimmetrikus trapéz területe tehát \(\displaystyle 5t/16\). Mivel \(\displaystyle DE:AB=1:4\), ezért \(\displaystyle EG:GA=DG:GB=1:4\). Emiatt az \(\displaystyle AGD\) és \(\displaystyle BGE\) háromszögek területe 4-szerese a \(\displaystyle DEG\) háromszög területének, az \(\displaystyle ABG\) háromszögé pedig 16-szorosa annak. Innen látszik, hogy a \(\displaystyle DGE\) háromszög területe az \(\displaystyle ABED\) trapéz területének \(\displaystyle 1/25\) része, vagyis \(\displaystyle t/80\). Ugyanez igaz az \(\displaystyle EFH\) és \(\displaystyle FDI\) háromszögekre is, vagyis a \(\displaystyle DGEHFI\) hatszög területe
\(\displaystyle \frac{t}{16}+3\cdot\frac{t}{80}=\frac{t}{10}.\)
A három tetraéder közös részének térfogata tehát \(\displaystyle 1/10\) része a tetraéder térfogatának.
Statisztika:
81 dolgozat érkezett. 4 pontot kapott: Ágoston Tamás, Árvay Balázs, Balási Szabolcs, Beke Lilla, Bencskó György Árpád, Botos Csongor, Böőr Katalin, Csere Kálmán, Csuka Róbert, Dudás 002 Zsolt, Dunay Luca, Éles András, Gyarmati Máté, Horváth János, Hosszejni Darjus, Janosov Milán, Janzer Olivér, Jéhn Zoltán, Karkus Zsuzsa, Karl Erik Holter, Keresztfalvi Tibor, Korondi Zénó, Köpenczei Gergő, Márkus Bence, Máthé László, Mester Márton, Mészáros András, Mihálka Éva Zsuzsanna, Nagy Róbert, Nagy-György Péter, Neukirchner Elisabeth, Perjési Gábor, Prok Tamás, Sándor Áron Endre, Strenner Péter, Szabó 928 Attila, Szőke Zsófia, Tamási Dénes, Trauttwein Klaudia, Uray Marcell János, Vuchetich Bálint, Weisz Ágoston. 3 pontot kapott: 9 versenyző. 2 pontot kapott: 16 versenyző. 1 pontot kapott: 12 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2009. szeptemberi matematika feladatai
