A B. 4203. feladat (2009. október)

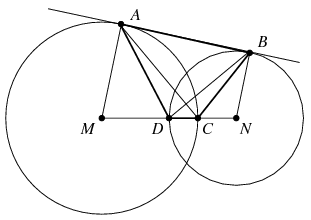
B. 4203. Két egymást metsző kört az egyik közös érintő az A és B pontokban érinti, a középpontjaikat összekötő szakasz pedig a C, illetve D pontokban metszi. Bizonyítsuk be, hogy ABCD húrnégyszög.

(4 pont)

A beküldési határidő 2009. november 10-én LEJÁRT.

Megoldás. A körök középpontját jelölje \(\displaystyle M\), illetve \(\displaystyle N\) az ábrán látható módon. Mivel \(\displaystyle BAC\sphericalangle+CAM\sphericalangle=90^\circ\), az \(\displaystyle AMC\) egyenlőszárú háromszögben \(\displaystyle AMC\sphericalangle= 180^\circ -2CAM\sphericalangle=2BAC\sphericalangle\). Hasonlóképpen, \(\displaystyle BND\sphericalangle=2ABC\sphericalangle\). Az \(\displaystyle AM\) és \(\displaystyle BN\) szakaszok párhuzamossága miatt \(\displaystyle AMC\sphericalangle+BND\sphericalangle=180^\circ\), ahonnan \(\displaystyle BAC\sphericalangle+ABC\sphericalangle=90^\circ\), vagyis az \(\displaystyle ABC\) háromszög a \(\displaystyle C\) csúcsnál derékszögű. Hasonlóképpen \(\displaystyle ADB\sphericalangle=90^\circ\) is igaz. A \(\displaystyle C\) és \(\displaystyle D\) pontok tehát az \(\displaystyle AB\) szakasz fölé emelt Thalesz-körön vannak, az \(\displaystyle ABCD\) négyszög valóban húrnégyszög.

Statisztika:

144 dolgozat érkezett.
4 pontot kapott:	97 versenyző.
3 pontot kapott:	13 versenyző.
2 pontot kapott:	5 versenyző.
1 pontot kapott:	5 versenyző.
0 pontot kapott:	17 versenyző.
Nem versenyszerű:	7 dolgozat.

A KöMaL 2009. októberi matematika feladatai