 |
A B. 4207. feladat (2009. október) |
B. 4207. Igaz-e, hogy minden sokszögnek van olyan csúcsa, amelyből húzható a sokszög belsejében haladó átló egy hozzá -- a nem szomszédosak közül -- legközelebb levő csúcsba?
Javasolta: Maga Péter
(4 pont)
A beküldési határidő 2009. november 10-én LEJÁRT.
Megoldás. Az állítás nem igaz, amint azt az alábbi ellenpélda mutatja. Vegyük fel az \(\displaystyle A,B,C,D\), \(\displaystyle E,F\) pontokat az ábrán látható módon úgy, hogy \(\displaystyle AF=AE=BE=BD=CD=1\) és \(\displaystyle AB=BC=DE=EF=\sqrt{2}\), ekkor \(\displaystyle AEF\), \(\displaystyle AEB\), \(\displaystyle BED\) és \(\displaystyle BDC\) egyenlőszárú derékszögű háromszögek.
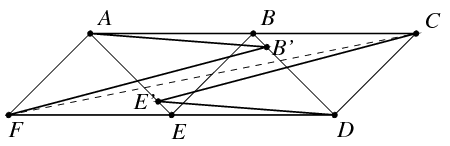
A \(\displaystyle CF\) szakasz \(\displaystyle BD\)-vel vett metszéspontját \(\displaystyle B\)-vel összekötő szakasz felezőpontja legyen \(\displaystyle B'\), \(\displaystyle E'\) pedig legyen ennek a pontnak a \(\displaystyle CF\) szakasz felezőpontjára vonatkozó tükörképe. Könnyen ellenőrizhetjük, hogy \(\displaystyle CF>DF=CA>B'F=CE'>DA>B'A=DE'>CB'>B'E'>CD>B'D\). Ezért az \(\displaystyle AB'FDE'C\) középpontosan szimmetrikus hatszögben a \(\displaystyle B'\) csúcshoz legközelebb eső csúcs \(\displaystyle D\), a \(\displaystyle C\) csúcshoz legközelebb eső csúcs \(\displaystyle D\), a \(\displaystyle D\) csúcshoz legközelebb eső csúcs pedig \(\displaystyle B'\), azonban sem a \(\displaystyle B'D\), sem a \(\displaystyle CD\) átló nem marad a sokszög belsejében. Az \(\displaystyle A,E',F\) csúcsok esetében pedig elegendő szimmetria okokra hivatkozni.
Statisztika:
68 dolgozat érkezett. 4 pontot kapott: Ábrahám Zsófia, Bálint Csaba, Bauer Barbara, Bősze Zsuzsanna, Csapó Botond Dániel, Cséke Balázs, Damásdi Gábor, Dudás 002 Zsolt, Éles András, Énekes Péter, Gyarmati Máté, Hajnal Péter János, Karkus Zsuzsa, Keresztfalvi Tibor, Kunos Vid, Márkus Bence, Mester Márton, Mészáros András, Nagy Róbert, Nagy-György Péter, Németh Bence, Perjési Gábor, Somogyi Ákos, Szenczi Zoltán, Varju 105 Tamás, Vogronics Patrik, Weisz Ágoston, Zelena Réka. 3 pontot kapott: Jaksa Péter, Magyari Ábel. 1 pontot kapott: 7 versenyző. 0 pontot kapott: 24 versenyző. Nem versenyszerű: 7 dolgozat.
A KöMaL 2009. októberi matematika feladatai
