 |
A B. 4284. feladat (2010. szeptember) |
B. 4284. Bizonyítsuk be, hogy egy érintőtrapéznak van olyan átlója, amelyik az alapokkal legfeljebb 45o-os szöget zár be.
(4 pont)
A beküldési határidő 2010. október 11-én LEJÁRT.
Megoldás. Az \(\displaystyle ABCD\) érintőtrapéz alapjai legyenek \(\displaystyle AB\) és \(\displaystyle CD\), magassága \(\displaystyle m\). A trapéz tükörképe a \(\displaystyle BC\) szár felezőpontjára nézve legyen \(\displaystyle A'CBD'\). Ekkor
\(\displaystyle 2m\le BC+AD=AB+CD=AD'.\)
A \(\displaystyle C\) csúcs \(\displaystyle C'\) merőleges vetülete az \(\displaystyle AB\) egyenesre az \(\displaystyle AD'\) szakasz belső pontja, hiszen a beírt kör \(\displaystyle AB\) szakaszra eső érintési pontja elválasztja az \(\displaystyle A\) és \(\displaystyle C'\) pontokat, tükörképének a \(\displaystyle BD'\) szakaszra eső érintési pontja pedig elválasztja a \(\displaystyle D'\) és \(\displaystyle C'\) pontokat az ábrán látható módon.
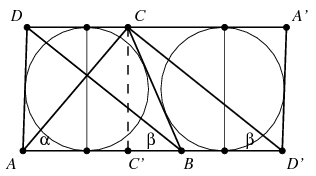
A fentiek miatt az \(\displaystyle AC'\) és \(\displaystyle D'C'\) szakaszok közül valamelyik legalább olyan hosszú, mint \(\displaystyle CC'\), és ezért az \(\displaystyle \alpha,\beta\) szögek közül a megfelelő nem nagyobb, mint \(\displaystyle 45^\circ\). A megoldásból az is látszik, hogy ha \(\displaystyle ABCD\) nem négyzet, akkor az egyik szög határozottan kisebb, mint \(\displaystyle 45^\circ\).
Statisztika:
95 dolgozat érkezett. 4 pontot kapott: Ágoston Péter, Balogh Adrienn Judit, Baráti László, Beke Lilla, Beleznay Soma, Bencze Tamás, Bogár-Szabó Tamás, Bősze Zsuzsanna, Czipó Bence, Damásdi Gábor, Énekes Péter, Fonyó Viktória, Gyarmati Máté, Homonnay Bálint, Janzer Olivér, Kabos Eszter, Kenéz Balázs, Kiss 542 Robin, Kovács 737 Ármin, Köpenczei Gergő, Kúsz Ágnes, Lenger Dániel, Máthé László, Mátrahegyi Roland, Medek Ákos, Mihálykó András, Nagy Róbert, Németh Krisztián, Ódor Gergely, Perjési Gábor, Rábai Domonkos, Schultz Vera Magdolna, Sieben Bertilla, Simig Dániel, Szabó 928 Attila, Tossenberger Tamás, Vajda Balázs, Varnyú József, Viharos Andor, Weisz Ambrus, Weisz Gellért, Wiandt Zsófia, Zilahi Tamás, Zsakó András. 3 pontot kapott: Bogár Blanka, Kiss 904 Tamara. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 10 versenyző. 0 pontot kapott: 36 versenyző.
A KöMaL 2010. szeptemberi matematika feladatai
