A B. 4286. feladat (2010. szeptember)

B. 4286. Egy egyenlő szárú derékszögű háromszög befogója 36 egység. Az egyik befogóra, a derékszögű csúcstól indítva, egymáshoz csatlakozó szabályos háromszögek végtelen sorozatát rajzoljuk úgy, hogy a beírt háromszögek harmadik csúcsa mindig illeszkedik az átfogóra, és ezen csúcsokkal szemközti oldalaik kitöltik a befogót. Határozzuk meg a szabályos háromszögek területének összegét.

(Kavics Kupa feladata nyomán)

(4 pont)

A beküldési határidő 2010. október 11-én LEJÁRT.

Megoldás. A derékszögű háromszög csúcsai legyenek az ábra szerint \(\displaystyle A,B,C\). Az \(\displaystyle AC\) befogóra rajzolt szabályos háromszögek közül a legnagyobbnak az egyik csúcsa \(\displaystyle C\) kell legyen, ez a \(\displaystyle CDX\) háromszög a végtelen sorozat első eleme.

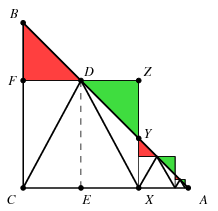
A \(\displaystyle D\) csúcs vetülete az \(\displaystyle AC,BC\) befogókra legyen \(\displaystyle E\), illetve \(\displaystyle F\), a \(\displaystyle DF\) egyenesre \(\displaystyle X\)-ben állított merőlegesnek az \(\displaystyle AB\) és \(\displaystyle DF\) egyenesekkel alkotott metszéspontja pedig \(\displaystyle Y\), illetve \(\displaystyle Z\). Mivel \(\displaystyle FD=CE=EX=DZ\), a \(\displaystyle BDF\) és \(\displaystyle YDZ\) egyenlő szárú derékszögű háromszögek egybevágók. Ezért a \(\displaystyle BCXY\) trapéz területe megegyezik az \(\displaystyle FCXZ\) téglalap területével, melynek pontosan a felét tölti ki a \(\displaystyle CDX\) háromszög.

Ha a végtelen sorozatban szereplő háromszögek \(\displaystyle AC\) befogóra eső csúcsaiban merőlegeseket állítunk az \(\displaystyle AC\) egyenesre, akkor ezek az \(\displaystyle ABC\) háromszöget a \(\displaystyle BCXY\) trapézhoz hasonló négyszögek végtelen sorozatára bontják úgy, hogy minden egyes háromszög az őt tartalmazó trapéz területének pontosan felét tölti ki. Ezért a szabályos háromszögek területének összege megegyezik az \(\displaystyle ABC\) háromszög területének felével, ami \(\displaystyle 36^2/4=18^2=324\) területegységet tesz ki.

Statisztika:

151 dolgozat érkezett.
4 pontot kapott:	85 versenyző.
3 pontot kapott:	39 versenyző.
2 pontot kapott:	10 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	11 versenyző.
Nem versenyszerű:	4 dolgozat.

A KöMaL 2010. szeptemberi matematika feladatai