 |
A B. 4287. feladat (2010. szeptember) |
B. 4287. Az ABC háromszög hozzáírt köreinek középpontja O1, O2 és O3. A háromszög egy, a beírt kör középpontjától különböző P belső pontjából a szögfelezőkre állított merőlegesek talppontjai M1, M2 és M3. Bizonyítsuk be, hogy az O1O2O3 és M1M2M3 háromszögek hasonlóak.
(5 pont)
A beküldési határidő 2010. október 11-én LEJÁRT.
Megoldás. Az ábrán az \(\displaystyle ABC\) háromszög külső és belső szögfelezőit rajzoltuk fel. Az \(\displaystyle O_1O_2O_3\) háromszög oldalegyenesei megegyeznek a külső szögfelezőkkel, míg a belső szögfelezők a beírt kör \(\displaystyle O\) középpontjában metszik egymást.
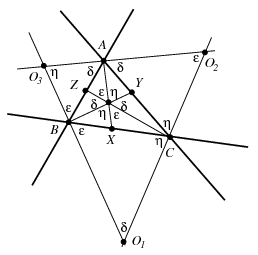
A szokásos jelölések mellett vezessük be a
\(\displaystyle \delta=\frac{\pi-\alpha}{2},\quad \varepsilon=\frac{\pi-\beta}{2},\quad \eta=\frac{\pi-\gamma}{2}\)
jelöléseket, e három szög összege éppen \(\displaystyle \pi\). Mivel az \(\displaystyle ABO_3\) háromszögben az \(\displaystyle A\)-nál és \(\displaystyle B\)-nél lévő szög \(\displaystyle \delta\), illetve \(\displaystyle \varepsilon\), a harmadik \(\displaystyle \eta\) kell legyen. A \(\displaystyle CZA\) háromszögben a \(\displaystyle Z\)-nél lévő szög \(\displaystyle \pi-\alpha-\frac{\gamma}{2}\), ezért az \(\displaystyle AOZ\) háromszögben az \(\displaystyle O\)-nál lévő szög
\(\displaystyle \pi-\frac{\alpha}{2}-\left(\pi-\alpha-\frac{\gamma}{2}\right)= \frac{\alpha}{2}+\frac{\gamma}{2}=\varepsilon<\frac{\pi}{2}.\)
Szimmetria okok miatt tehát az \(\displaystyle O_1O_2O_3\) háromszög szögei éppen \(\displaystyle \delta,\varepsilon,\eta\), és ugyanezek a szögek lépnek fel a belső szögfelezők között is. Vizsgáljuk most az \(\displaystyle M_1M_2M_3\) háromszöget. Az egyszerűség kedvéért tegyük fel, hogy az \(\displaystyle O\), \(\displaystyle P\), \(\displaystyle M_1\), \(\displaystyle M_2\) és \(\displaystyle M_3\) pontok mind különböznek egymástól. (A kivételes esetek azok, amikor \(\displaystyle P\) valamelyik szögfelezőre, vagy valamelyik szögfelezőre merőleges \(\displaystyle O\)-n áthaladó egyenesre esik; ezeket az eseteket akár egy folytonossági meggondolással is elintézhetjük.)
Az általánosság megszorítása nélkül feltehetjük, hogy \(\displaystyle P\) az \(\displaystyle OBX\) háromszög belső pontja. Mivel ennek \(\displaystyle O\)-nál lévő szöge hegyesszög, az \(\displaystyle A\)-ból és a \(\displaystyle B\)-ből induló szögfelezőre eső vetületek az \(\displaystyle OX\) félegyenesre, illetve az \(\displaystyle OB\) szakaszra esnek, a \(\displaystyle C\)-ből induló szögfelezőre eső vetület pedig aszerint esik az \(\displaystyle OZ\) félegyenesre vagy az \(\displaystyle OC\) szakaszra, hogy a \(\displaystyle P\) pont az ezen szögfelezőre merőleges \(\displaystyle O\)-n áthaladó egyenes melyik oldalára esik. Ennek alapján az alábbi két ábra valamelyike érvényes.
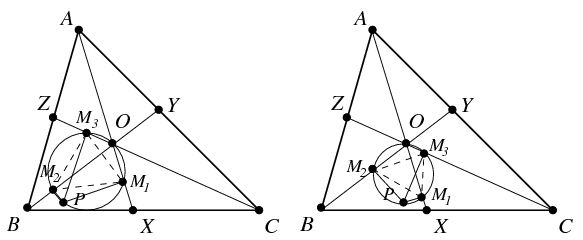
A Thalesz-tétel megfordítása szerint az \(\displaystyle M_1\), \(\displaystyle M_2\), \(\displaystyle M_3\) pontok az \(\displaystyle OP\) átmérőjű körvonalra esnek. A kerületi szögek tétele alapján az első esetben
\(\displaystyle M_3M_1M_2\angle=M_3OM_1\angle=ZOB\angle=\delta,\quad M_2M_3M_1\angle=M_2OM_1\angle=BOX\angle=\eta.\)
A második esetben pedig
\(\displaystyle M_1M_2M_3\angle=M_1OM_3\angle=XOC\angle=\varepsilon,\quad M_2M_3M_1\angle=M_2OM_1\angle=BOX\angle=\eta.\)
Az \(\displaystyle M_1M_2M_3\) háromszög szögei tehát mindkét esetben megegyeznek az \(\displaystyle O_1O_2O_3\) háromszög szögeivel.
Statisztika:
58 dolgozat érkezett. 5 pontot kapott: Bálint Csaba, Boér Lehel, Csuka Róbert, Dobosy Kristóf, Fonyó Viktória, Janzer Olivér, Kiss Boldizsár, Köpenczei Gergő, Lajos Mátyás, Schultz Vera Magdolna, Strenner Péter, Szabó 777 Bence, Szabó 928 Attila, Varnyú József. 4 pontot kapott: Barczel Nikolett, Beke Lilla, Bogár Blanka, Bősze Zsuzsanna, Bunth Gergely, Csörgő András, Damásdi Gábor, Dinev Georgi, Énekes Péter, Freud Edvin, Gyarmati Máté, Győrfi 946 Mónika, Hajnal Máté, Kabos Eszter, Karl E. Holter, Kenéz Balázs, Kovács 444 Áron, Máthé László, Medek Ákos, Molnár Ákos, Müller Dóra Tímea, Nagy 111 Miklós, Nagy Dániel Bálint, Nagy Róbert, Neukirchner Elisabeth, Rábai Domonkos, Szende Tamás, Vajda Balázs, Vajk Dóra, Varga 911 Szabolcs, Viharos Andor, Weisz Gellért, Zahemszky Péter, Zelena Réka. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2010. szeptemberi matematika feladatai
