A B. 4299. feladat (2010. október)

B. 4299. Az ABC háromszögbe írt CDEF paralelogramma D, E, F csúcsa rendre a CA, AB és BC oldalon van. Szerkesszük meg a DF szakasz hosszának ismeretében az E pontot. Melyik E pontra lesz a DF átló hossza minimális?

dr. Katz Sándor (Bonyhád)

(5 pont)

A beküldési határidő 2010. november 10-én LEJÁRT.

Megoldás. Az \(\displaystyle AB,BC,CA\) oldalak felezőpontját jelölje rendre \(\displaystyle X,Y,Z\), az \(\displaystyle EF\) szakasz felezőpontját pedig \(\displaystyle H\). Mivel \(\displaystyle H\) egyben a \(\displaystyle CD\) szakasz felezőpontja is, a \(\displaystyle H\) pont illeszkedik a háromszög \(\displaystyle YZ\) középvonalára. Ha az \(\displaystyle EF\) szakasz egybeesik az \(\displaystyle YZ\) szakasszal, akkor \(\displaystyle D=X\). Tegyük fel, hogy \(\displaystyle E\) az \(\displaystyle YC\), \(\displaystyle F\) pedig az \(\displaystyle AZ\) szakasz belső pontja. Az \(\displaystyle F\) pont \(\displaystyle Z\)-re vonatkozó tükörképe legyen \(\displaystyle F'\), az \(\displaystyle EF'\) szakasz felezőpontja pedig \(\displaystyle H'\). Ekkor \(\displaystyle HZ\), \(\displaystyle ZH'\) és \(\displaystyle HH'\) az \(\displaystyle EFF'\) háromszög középvonalai.

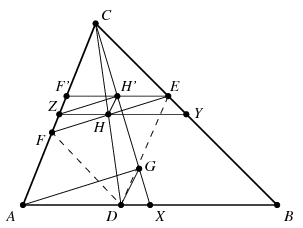
A \(\displaystyle ZHH'\) háromszöget \(\displaystyle C\)-ből kétszeresére nagyítva azt az \(\displaystyle ADG\) háromszöget kapjuk, amelynek \(\displaystyle G\) csúcsa a \(\displaystyle CX\) szakasz belső pontja és \(\displaystyle \overrightarrow{AG}=\overrightarrow{FE}\). Megfordítva, ha \(\displaystyle G\) a \(\displaystyle CX\) szakasz olyan pontja, amelyre \(\displaystyle AG=EF\), akkor ehhez egyértelműen tartozik egy megfelelő \(\displaystyle DECF\) paralelogramma.

Ezek alapján a szerkesztés a következőképpen végezhető el. Az \(\displaystyle A\) csúcs, mint középpont köré \(\displaystyle EF\) sugarú kört rajzolunk, ez a \(\displaystyle CX\) egyenest 0, 1 vagy 2 pontban metszi. Nyilván ugyanezeket a metszéspontokat kapjuk akkor is, ha a \(\displaystyle B\) csúcsot választjuk középpontnak. Válasszuk ki ezek közül azokat a \(\displaystyle G\) pontokat, amelyek a \(\displaystyle CX\) szakaszra esnek, de nem esnek egybe \(\displaystyle C\)-vel. Ha \(\displaystyle AG=EF\), akkor a \(\displaystyle G\)-n keresztül \(\displaystyle AC\)-vel párhuzamosan húzott egyenes metszi ki az \(\displaystyle AB\) szakaszból a \(\displaystyle D\) pontot, ha pedig \(\displaystyle BG=EF\), akkor a \(\displaystyle G\)-n keresztül \(\displaystyle BC\)-vel párhuzamosan húzott egyenes metszi ki az \(\displaystyle AB\) szakaszból a \(\displaystyle D\) pontot.

Az \(\displaystyle EF\) átló hossza nyilván akkor minimális, ha \(\displaystyle G\) a lehető legközelebb esik az \(\displaystyle A,B\) csúcsok valamelyikéhez, vagyis ha \(\displaystyle AG\) vagy \(\displaystyle BG\) merőleges \(\displaystyle CX\)-re. Tegyük fel, hogy \(\displaystyle CA\le CB\), és legyen \(\displaystyle G_0\) az \(\displaystyle A\) pontból az \(\displaystyle CX\) egyenesre állított merőleges talppontja. Ekkor \(\displaystyle G_0\)-ból \(\displaystyle AC\)-vel párhuzamost húzva metszhetjük ki az \(\displaystyle AB\) szakaszból a keresett \(\displaystyle D\) pontot.

Mindezek figyelembevételével a \(\displaystyle CA\le CB\) feltevés mellett a feladat diszkussziója a következő. Ha az adott \(\displaystyle EF\) távolság kisebb, mint \(\displaystyle AG_0\), akkor a feladatnak nincsen megoldása. \(\displaystyle EF=AG_0\) esetén pontosan egy megoldás van, ez a helyzet speciálisan az \(\displaystyle AC=AB\) esetben is. Ha \(\displaystyle AG_0<EF<AC\), akkor két megoldást kapunk, \(\displaystyle AC\le EF< BC\) esetén megint csak egyet, \(\displaystyle BC\le EF\) esetén pedig ismétcsak nem lesz megoldás.

A letölthető GeoGebra ábra Tossenberger Tamás munkája: B.4299.html

Statisztika:

30 dolgozat érkezett.
5 pontot kapott:	Böőr Katalin, Bősze Zsuzsanna, Damásdi Gábor, Énekes Péter, Kabos Eszter, Kiss 542 Robin, Lajos Mátyás, Medek Ákos, Nagy Balázs, Nagy Róbert, Tossenberger Tamás, Varnyú József, Viharos Andor.
4 pontot kapott:	Dudás 002 Zsolt, Janzer Olivér, Lenger Dániel, Perjési Gábor, Weisz Gellért.
3 pontot kapott:	4 versenyző.
2 pontot kapott:	1 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	3 versenyző.

A KöMaL 2010. októberi matematika feladatai