A B. 4335. feladat (2011. február)

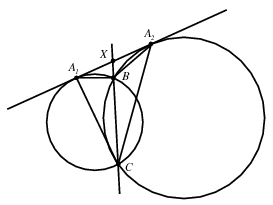
B. 4335. Két, egymást a B és C pontokban metsző kört egy egyenes az A₁ és A₂ pontokban érint. Bizonyítsuk be, hogy

Javasolta: Mester Márton (Szeged)

(4 pont)

A beküldési határidő 2011. március 10-én LEJÁRT.

Megoldás. A $\displaystyle BC$ egyenesnek az $\displaystyle A_1A_2$ szakasszal vett metszéspontját jelölje $\displaystyle X$. A kerületi szögek tétele szerint a $\displaystyle BCA_i$ szög egyenlő a $\displaystyle BA_iX$ szöggel, ezért az $\displaystyle XCA_i$ háromszög hasonló az $\displaystyle XA_iB$ háromszöghöz, tehát $\displaystyle XC:A_iX=A_iX:XB$. A szinusz-tételt felhasználva kapjuk, hogy

$\displaystyle \frac{A_iB}{A_iC} = \frac{\sin BCA_i\sphericalangle}{\sin CBA_i\sphericalangle}=\frac{\sin BA_iX\sphericalangle}{\sin XBA_i\sphericalangle}=\frac{XB}{A_iX}.$

Elegendő tehát azt igazolni, hogy $\displaystyle A_1X=A_2X$, ami viszont azonnal leolvasható az $\displaystyle A_iX^2=XB\cdot XC$ összefüggésből.

Statisztika:

46 dolgozat érkezett.
4 pontot kapott:	Baráti László, Barczel Nikolett, Beke Lilla, Boér Lehel, Bogár Blanka, Bősze Zsuzsanna, Damásdi Gábor, Dobos Nóra, Dobosy Kristóf, Dolgos Tamás, Emri Tamás, Énekes Péter, Fonyó Viktória, Frank Evelyn, Frittmann Júlia, Győrfi 946 Mónika, Hajnal Máté, Halász Dániel, Hopp Norbert, Kovács Márton, Máthé László, Medek Ákos, Müller Dóra Tímea, Nagy Zsanett, Rábai Domonkos, Sagmeister Ádám, Strenner Péter, Szabó 928 Attila, Tekeli Tamás, Tossenberger Tamás, Tulassay Zsolt, Varga 515 Balázs, Varga 911 Szabolcs, Weimann Richárd, Weisz Gellért, Wiandt Zsófia, Zilahi Tamás, Zsakó András.
3 pontot kapott:	Dunay Luca, Lajos Mátyás, Magyari Ábel, Nagy Balázs, Temesvári Eszter, Tran Trong Hoang Tuan.
0 pontot kapott:	2 versenyző.

A KöMaL 2011. februári matematika feladatai