 |
A B. 4336. feladat (2011. február) |
B. 4336. Az ABCD parallelogramma AB és BC oldalára kifelé szabályos háromszöget szerkesztünk, ezek harmadik csúcsa E, illetve F. Mutassuk meg, hogy a CED és AFD szögek összege 60o.
Javasolta: Miklós Szilárd (Herceghalom)
(4 pont)
A beküldési határidő 2011. március 10-én LEJÁRT.
Megoldás. Mivel \(\displaystyle AD=CF\), \(\displaystyle AE=CD\), valamint az \(\displaystyle DAE\) és \(\displaystyle FCD\) szögek is egyenlők, látható, hogy a \(\displaystyle DAE\) és \(\displaystyle FCD\) háromszögek egybevágók, tehát \(\displaystyle DE=DF\).
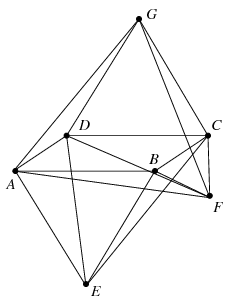
A \(\displaystyle CBE\) háromszöget \(\displaystyle B\) körül (óramutató járásával megegyező irányban) \(\displaystyle 60^\circ\)-os szöggel elforgatva kapjuk az \(\displaystyle FBA\) háromszöget. Ha ezt a háromszöget \(\displaystyle F\) körül forgatjuk el \(\displaystyle 60^\circ\)-os szöggel, az \(\displaystyle FCG\) háromszöghöz jutunk. Az így nyert \(\displaystyle G\) pontra teljesül tehát, hogy \(\displaystyle CE=FA=FG\), továbbá hogy mind az \(\displaystyle AFG\), mind a \(\displaystyle DCG\) háromszög is szabályos, vagyis \(\displaystyle DC=DG\) is teljesül.
Mindezeket egybevetve kapjuk, hogy a \(\displaystyle DEC\) és \(\displaystyle DFG\) háromszögek egybevágók, következésképpen
\(\displaystyle AFD\sphericalangle+CED\sphericalangle=AFD\sphericalangle+DFG\sphericalangle=AFG\sphericalangle=60^\circ.\)
Statisztika:
102 dolgozat érkezett. 4 pontot kapott: Ágoston Péter, Baráti László, Bogár Blanka, Bősze Zsuzsanna, Czipó Bence, Dolgos Tamás, Fonyó Viktória, Herczeg József, Homonnay Bálint, Kenéz Balázs, Klincsik Gergely, Lenger Dániel, Mihálykó András, Molnár Ákos, Sagmeister Ádám, Scharle Csilla, Schultz Vera Magdolna, Schwarcz Gergő, Strenner Péter, Szabó 928 Attila, Varjú János, Viharos Andor, Weisz Ambrus, Weisz Gellért. 3 pontot kapott: 63 versenyző. 2 pontot kapott: 11 versenyző. 1 pontot kapott: 2 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2011. februári matematika feladatai
