 |
A B. 4408. feladat (2011. december) |
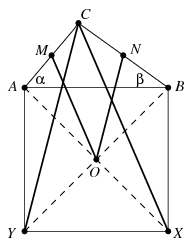
B. 4408. Az ABC háromszögben AC és BC oldalak hossza rögzített, a C-nél levő szög pedig változik. Az AC oldal felezőpontja M, a BC oldal felezőpontja N, az AB oldalra kifelé állított négyzet középpontja pedig O. Hogyan kell az ACB szöget megválasztani ahhoz, hogy az OM és ON távolságok összege a lehető legnagyobb legyen?
(4 pont)
A beküldési határidő 2012. február 10-én LEJÁRT.
Megoldás. A négyzet másik két csúcsát \(\displaystyle X\) és \(\displaystyle Y\) jelöli az ábra szerint, akkor az \(\displaystyle OM\) szakasz az \(\displaystyle AXC\), \(\displaystyle ON\) pedig a \(\displaystyle BYC\) háromszög középvonala, tehát \(\displaystyle OM+ON=(XC+YC)/2\), vagyis az \(\displaystyle XC+YC\) összeget szeretnénk maximalizálni. A szokásos jelölésekkel a \(\displaystyle BXC\) háromszögre a koszinusz-tételt felírva kapjuk, hogy
\(\displaystyle CX^2=a^2+c^2-2ac\cos(\beta+90^\circ)= a^2+c^2+2ac\sin\beta=a^2+c^2+2ab\sin\gamma,\)
hiszen a szinusz-tétel szerint \(\displaystyle c\sin\beta=b\sin\gamma\).
Ugyanígy \(\displaystyle CY^2=b^2+c^2+2ab\sin\gamma\). Lévén \(\displaystyle c^2=a^2+b^2-2ab\cos\gamma\),
\(\displaystyle XC+YC=\sqrt{2a^2+b^2+2ab(\sin\gamma-\cos\gamma)}+ \sqrt{a^2+2b^2+2ab(\sin\gamma-\cos\gamma)}.\)
Világos, hogy ez a kifejezés akkor veszi fel a maximumát, ha \(\displaystyle \sin\gamma-\cos\gamma\) értéke a lehető legnagyobb. Minthogy
\(\displaystyle \sin\gamma-\cos\gamma=\sqrt{2}\sin(\gamma-45^\circ),\)
ez nyilván \(\displaystyle \gamma=135^\circ\) esetén következik be.
Statisztika:
29 dolgozat érkezett. 4 pontot kapott: Bingler Arnold, Czipó Bence, Fehér Zsombor, Fonyó Viktória, Janzer Olivér, Jávorszky Natasa, Kaprinai Balázs, Kiss 902 Melinda Flóra, Lucskai Gábor, Machó Bónis, Mester Márton, Mihálykó András, Ódor Gergely, Sticza Gergő, Strenner Péter, Szabó 928 Attila, Weimann Richárd. 3 pontot kapott: Árkos Gergely, Nagy-György Pál, Schultz Vera Magdolna, Somogyvári Kristóf, Szilágyi Gergely Bence. 2 pontot kapott: 4 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 2 versenyző.
A KöMaL 2011. decemberi matematika feladatai
