 |
A B. 4426. feladat (2012. február) |
B. 4426. Az ABCD tetraéder szemközti élei merőlegesek egymásra, BCD lapja pedig hegyesszögű háromszög. A tetraéder A csúcsból induló magasságának talppontja T. Adjuk meg a tetraéder felszínén haladó legrövidebb AT töröttvonalat.
(4 pont)
A beküldési határidő 2012. március 12-én LEJÁRT.
Megoldás. Legyen \(\displaystyle \{X,Y,Z\}=\{B,C,D\}\). Mivel \(\displaystyle AX\) merőleges \(\displaystyle YZ\)-re, az \(\displaystyle AX\) egyenest tartalmazó, \(\displaystyle BCD\) síkra merőleges sík az \(\displaystyle YZ\) egyenest abban az \(\displaystyle X'\) pontban metszi,
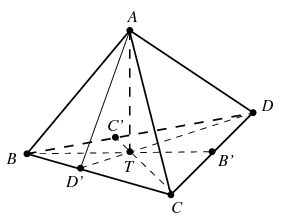
amelyre \(\displaystyle X'\) az \(\displaystyle YZA\) és az \(\displaystyle YZX\) háromszögben egyaránt az \(\displaystyle YZ\)-re merőleges magasság talppontja. Minthogy ez utóbbi háromszög hegyesszögű, az \(\displaystyle X'\) pont az \(\displaystyle YZ\) szakasz belső pontja, és az is világos, hogy \(\displaystyle T\) éppen a \(\displaystyle BCD\) háromszög magasságpontja. Azon \(\displaystyle AT\) töröttvonalak közül pedig, melyek az \(\displaystyle YZ\) szakaszt metszik, éppen az \(\displaystyle AX'T\) töröttvonal lesz a legrövidebb. Azt kell tehát eldöntenünk, hogy az \(\displaystyle AB'T, AC'T, AD'T\) töröttvonalak közül melyik a legrövidebb. Mivel a Pithagorasz-tétel szerint az \(\displaystyle AX'T\) töröttvonal hossza
\(\displaystyle AX'+X'T=\sqrt{AT^2+X'T^2}+X'T,\)
a \(\displaystyle B'T, C'T, D'T\) szakaszok közül kell a legrövidebbet kiválasztanunk. Ehhez tekintsük a \(\displaystyle TB'C\) és \(\displaystyle TD'C\) derékszögű háromszögeket. Mivel ezek \(\displaystyle TC\) átfogója közös, a \(\displaystyle TB',TD'\) befogók közül az rövidebb, amely mellett nagyobb szög van. ám \(\displaystyle B'TC\sphericalangle=CDB\sphericalangle\) és \(\displaystyle D'TC\sphericalangle=CBD\sphericalangle\), és a \(\displaystyle BCD\) háromszögben a hosszabb oldallal szemben van a nagyobb szög, vagyis \(\displaystyle B'T\le D'T\) pontosan akkor teljesül, ha \(\displaystyle BC\ge DC\). A \(\displaystyle B'T, D'T\) szakaszokat hasonlóképpen \(\displaystyle C'T\)-vel is összehasonlítva láthatjuk, hogy a \(\displaystyle T\) pont a \(\displaystyle BCD\) háromszög oldalai közül a legrövidebbhez van a legközelebb. A legrövidebb \(\displaystyle AT\) töröttvonalat tehát úgy kapjuk, hogy \(\displaystyle A\)-ból merőlegest bocsájtunk a \(\displaystyle BCD\) háromszög legrövidebb oldalára, majd az így kapott pontot \(\displaystyle T\)-vel összekötjük. Ennek megfelelően 1, 2 vagy 3 megoldást kapunk aszerint, hogy a \(\displaystyle BCD\) háromszög általános, általános egyenlő szárú vagy pedig szabályos.
Statisztika:
43 dolgozat érkezett. 4 pontot kapott: Ágoston Péter, Babik Bálint, Bingler Arnold, Bősze Zsuzsanna, Czipó Bence, Demeter Dániel, Englert Franciska, Forrás Bence, Frank György, Janzer Olivér, Jenei Adrienn, Kabos Eszter, Kecskés Boglárka, Maga Balázs, Mester Márton, Nagy Anna Noémi, Ódor Gergely, Papp Roland, Sagmeister Ádám, Schultz Vera Magdolna, Schwarcz Tamás, Strenner Péter, Szabó 262 Lóránt, Szabó 789 Barnabás, Tardos Jakab, Thamó Emese, Weimann Richárd, Zilahi Tamás. 3 pontot kapott: Badacsonyi István András, Dinev Georgi, Győrfi 946 Mónika, Kacz Dániel, Medek Ákos. 2 pontot kapott: 3 versenyző. 1 pontot kapott: 4 versenyző. 0 pontot kapott: 3 versenyző.
A KöMaL 2012. februári matematika feladatai
