A B. 4463. feladat (2012. szeptember)

B. 4463. A Négyszögletű Kerek Erdő fái egy szabályos háromszögrács rácspontjain állnak. El lehet-e keríteni az erdőből egy téglalap alakú részt úgy, hogy a téglalap csúcsai rácspontok legyenek, és a téglalap határán ugyanannyi rácspont legyen, mint a belsejében?

(4 pont)

A beküldési határidő 2012. október 10-én LEJÁRT.

Megoldás. Igen (feltéve, hogy az erdő elég nagy). Egy ilyen elkerített rész látható az ábrán, ahol mind a téglalap határán, mind annak belsejében egyaránt 14 fa áll.

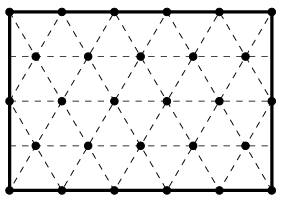
Ezt a téglalapot az alábbi gondolatmenettel találhatjuk meg. Legyen a rácspontok távolsága egységnyi és kerítsünk körbe egy -es téglalapot úgy, hogy k,n pozitív egészek és a k hosszú oldalakon, a végpontokat is beleértve, egyenként k+1 rácspont van. Ekkor az összes bekerített rácspont száma (k+1)(n+1)+kn, a határon lévők száma pedig 2(k+n), vagyis a (k+1)(n+1)+kn=4(k+n) egyenletet kell megoldanunk. Ez ekvivalens a (3k-1)(3n-1)=7kn egyenlettel, ahol 3k-1 relatív prím k-hoz, 3n-1 pedig n-hez. Tehát vagy k=3n-1 és 3k-1=7n, vagy fordítva. Az első esetben n=2 és k=5, ez látható az ábrán.

Statisztika:

209 dolgozat érkezett.
4 pontot kapott:	65 versenyző.
3 pontot kapott:	27 versenyző.
2 pontot kapott:	78 versenyző.
1 pontot kapott:	20 versenyző.
0 pontot kapott:	19 versenyző.

A KöMaL 2012. szeptemberi matematika feladatai