A B. 4468. feladat (2012. szeptember)

B. 4468. Adott két körlemez, melyeknek nincs közös pontja. A körök középpontjait összekötő szakasz, mint átmérő fölé rajzolt kör a két közös külső érintőt két-két pontban metszi. Bizonyítsuk be, hogy ezen négy pont által meghatározott négyszög átlói a körök közös belső érintői.

Javasolta: Gedeon Veronika (Budapest)

(5 pont)

A beküldési határidő 2012. október 10-én LEJÁRT.

Megoldás. A körök közös belső érintői a külső érintőket két-két pontban metszik. A bizonyítandó állítást úgy is fogalmazhatjuk, hogy ezen négy pont mindegyike a körök középpontjait összekötő szakasz, mint átmérő fölé rajzolt körvonalra esik. Szimmetria okok miatt ezt elég az egyik metszéspontra igazolni, melyet jelöljön M.

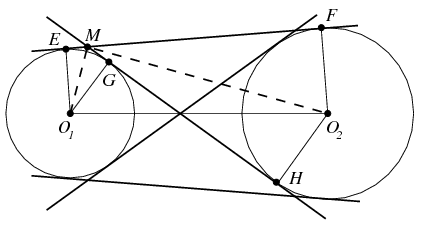
Az ábra jelöléseivel legyen $GO_1O_2\sph=HO_2O_1\sph=\alpha$ , $FO_2O_1\sph=180^\circ-EO_1O_2\sph=\beta$ . Ha a két kör ugyanakkora, akkor $\beta$ derékszög, ha a jobb oldali kör a kisebb, akkor $\beta$ tompaszög, mindenesetre $\alpha$ < $\beta$ <180^o- $\alpha$ . Minthogy az O₂M egyenes felezi az FO₂H szöget, O₁M pedig az EO₁G szöget,

$O_1O_2M\sph=\frac{\alpha+\beta}{2}-\alpha, \qquad O_2O_1M\sph=\alpha+\frac{(180^\circ-\beta)-\alpha}{2}.$

A két szög összege 90^o, vagyis az O₁O₂M háromszög M-nél lévő szöge derékszög. Ez pedig Thalész tétele szerint pontosan azt jelenti, hogy M az O₁O₂ átmérőjű körvonalra esik.

Statisztika:

83 dolgozat érkezett.

5 pontot kapott: 58 versenyző.

4 pontot kapott: 13 versenyző.

3 pontot kapott: 3 versenyző.

2 pontot kapott: 2 versenyző.

1 pontot kapott: 2 versenyző.

0 pontot kapott: 5 versenyző.

A KöMaL 2012. szeptemberi matematika feladatai

83 dolgozat érkezett.
5 pontot kapott:	58 versenyző.
4 pontot kapott:	13 versenyző.
3 pontot kapott:	3 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	2 versenyző.
0 pontot kapott:	5 versenyző.

Már regisztráltál?
Új vendég vagy?