Problem B. 4510. (January 2013)

B. 4510. The length of the base edges of a right regular pyramid of (2k+1) sides is 1, the centre of the base is O, and the length of the altitude OB is m. The pyramid is reflected in the midpoint of OB. Find the volume of the intersection of the two pyramids.

(6 pont)

Deadline expired on February 11, 2013.

Sorry, the solution is available only in Hungarian. Google translation

Megoldási ötlet: A gúlák közös tengelyére illeszkedő félsíkokkal bontsuk részekre a gúlákat és a közös részüket (mint egy tortát), és számítsuk ki a térfogatokat egy-egy szeletben.

Megoldás. Legyen a gúla alaplapja $A_0A_1\ldots A_{2k}$ , a tükörkép alaplapja $C_0C_1\ldots C_{2k}$ , csúcsa O. Az alaplapok csúcsait modulo 2k+1 fogjuk indexelni, tehát például A_2k+1=A₀.

Legyen az A_iA_i+1 él felezőpontja F_i, a C_iC_i+1 él felezőpontja pedig G_i. Például az A_iF_iO derékszögű háromszögekből leolvashatjuk, hogy az alaplapok köré írt kör sugara

$R=\dfrac1{2\sin{\frac{180^\circ}{2k+1}}},$

a beírt körök sugara pedig

$r=\frac12 \ctg\frac{180^\circ}{2k+1} = \frac{\cos\frac{180^\circ}{2k+1}}{2\sin\frac{180^\circ}{2k+1}}.$

A B, O, A_i és G_k+i pontok egy síkba esnek, mert C_iBG_k+i $\angle$ =180^o; legyen U_i=A_iB $\cap$ G_k+iO. Hasonlóan legyen V_i=F_iB $\cap$ C_k+i+1O.

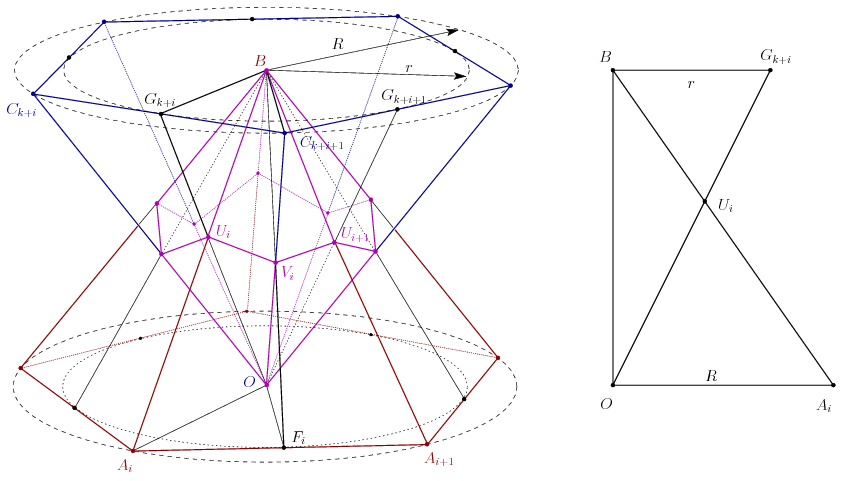
Tekintsük most a gúláknak és a metszetüknek a BOA_iG_k+i és BOF_iC_k+i+1 félsíkok közé eső részét. A közös részt a két félsík, továbbá az A_iA_i+1B és C_k+iC_k+i+1O lapok határolják, a közös rész tehát egy tetraéder, amelynek csúcsai B, O, U_i és V_i.

A BOU_iV_i tetraéder térfogatát a BOA_iF_i tetraéder térfogatával fogjuk összehasonlítani. A OA_iG_k+iB derékszögű trapéz alapjainak hossza OA_i=R és G_k+iB=r, az átlók metszéspontja U_i. A OA_iU_i és G_k+iBU_i háromszögek hasonlók, így $\dfrac{A_iU_i}{BU_i}= \dfrac{OA_i}{G_{k+i}B}=\dfrac{r}{R}$ , és

$\frac{BU_i}{BA_i} = \frac{BU_i}{BU_i+U_iA_i} = \dfrac{r}{R+r}.$

Hasonlóan, a OF_iC_k+i+1B trapéz vizsgálatából kapjuk, hogy

$\frac{BV_i}{BF_i} = \dfrac{R}{R+r}.$

Ezek után

$\dfrac{{\rm t\'erfogat}(BOU_iV_i)}{{\rm t\'erfogat}(BOA_iF_i)} = \frac{BU_i}{BA_i} \cdot \frac{BV_i}{BF_i} = \dfrac{Rr}{(R+r)^2}.$

A szimmetria miatt az arány mindegyik térrészben ugyanaz. Ezért a két gúla közös részének térfogata

$\dfrac{Rr}{(R+r)^2} \cdot {\rm t\'erfogat}(A_0A_1\ldots A_{2k}P) = \dfrac{Rr}{(R+r)^2} \cdot \left(\frac13\cdot(2k+1)\frac{r}2 \cdot m\right) =$

$= \dfrac{(2k+1)m}6 \cdot \dfrac{R r^2}{(R+r)^2} = \dfrac{(2k+1)m\cos^2\frac{180^\circ}{2k+1} }{12\sin\frac{180^\circ}{2k+1}(1+\cos\frac{180^\circ}{2k+1})^2}.$

Statistics:

27 students sent a solution.

6 points: Balogh Tamás, Fehér Zsombor, Forrás Bence, Havasi 0 Márton, Janzer Olivér, Maga Balázs, Schwarcz Tamás, Tardos Jakab, Tossenberger Tamás, Venczel Tünde.

5 points: Ágoston Péter, Herczeg József, Lelkes János, Medek Ákos, Németh Gergely, Paulovics Zoltán, Simkó Irén, Szabó 789 Barnabás.

4 points: 3 students.

3 points: 1 student.

2 points: 1 student.

1 point: 4 students.

Problems in Mathematics of KöMaL, January 2013

27 students sent a solution.
6 points:	Balogh Tamás, Fehér Zsombor, Forrás Bence, Havasi 0 Márton, Janzer Olivér, Maga Balázs, Schwarcz Tamás, Tardos Jakab, Tossenberger Tamás, Venczel Tünde.
5 points:	Ágoston Péter, Herczeg József, Lelkes János, Medek Ákos, Németh Gergely, Paulovics Zoltán, Simkó Irén, Szabó 789 Barnabás.
4 points:	3 students.
3 points:	1 student.
2 points:	1 student.
1 point:	4 students.

Already signed up?
New to KöMaL?