Középiskolai Matematikai és Fizikai Lapok
Informatika rovattal
Kiadja a MATFUND Alapítvány
Már regisztráltál?
Új vendég vagy?

A B. 4534. feladat (2013. április)

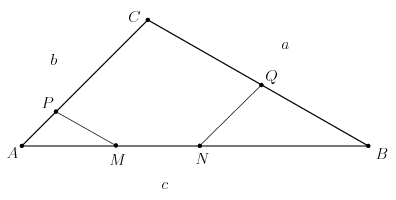
B. 4534. Az ABC háromszög leghosszabb, AB oldalán levő M és N pontokra teljesül, hogy BM=BC és AN=AC. Az M ponton át a BC oldallal húzott párhuzamos az AC oldalt P-ben, az N ponton át az AC oldallal húzott párhuzamos a BC oldalt Q-ban metszi. Bizonyítsuk be, hogy CP=CQ.

(Kvant)

(3 pont)

A beküldési határidő 2013. május 10-én LEJÁRT.

Megoldási ötlet: Párhuzamos szelők tétele.

Megoldás. Legyenek a háromszög oldalai BC=a, CA=b és AB=c. A párhuzamos szelők tételét alkamazva, \frac{CP}{AC} = \frac{BM}{AB}, amiből

CP = \frac{BM\cdot AC}{AB} = \frac{BC\cdot AC}{AB} = \frac{ab}{c}.

Hasonlóan kapjuk, hogy \frac{CQ}{CB} = \frac{AN}{AB}, és

CQ = \frac{AN\cdot CB}{AB} = \frac{AC\cdot CB}{AB} = \frac{ba}{c}.

Tehát CP=CQ=\frac{ab}c.

Statisztika:

100 dolgozat érkezett.
3 pontot kapott:94 versenyző.
2 pontot kapott:1 versenyző.
1 pontot kapott:2 versenyző.
0 pontot kapott:3 versenyző.

A KöMaL 2013. áprilisi matematika feladatai