A B. 4539. feladat (2013. április)

B. 4539. Az ABC háromszög súlypontja S, köréírt körének középpontja K. A BCS, CAS és ABS háromszögek köré írt körök középpontjai P, Q és R. Bizonyítsuk be, hogy a PQR háromszög súlypontja K.

Javasolta: Sárosdi Zsombor (Veresegyház)

(5 pont)

A beküldési határidő 2013. május 10-én LEJÁRT.

Megoldás: A $\displaystyle PQR$ háromszög oldalai az $\displaystyle SA$, $\displaystyle SB$, $\displaystyle SC$ szakaszok felezőmerőlegesei. Elegendő megmutatni, hogy az $\displaystyle ABC$ háromszög oldalfelező merőlegesei a $\displaystyle PQR$ háromszög súlyvonalai, hiszen ekkor a három egyenes közös $\displaystyle K$ pontja a $\displaystyle PQR$ háromszög súlypontja lesz. Ezt szimmetria okok miatt elég egy felezőmerőlegesre bizonyítani.

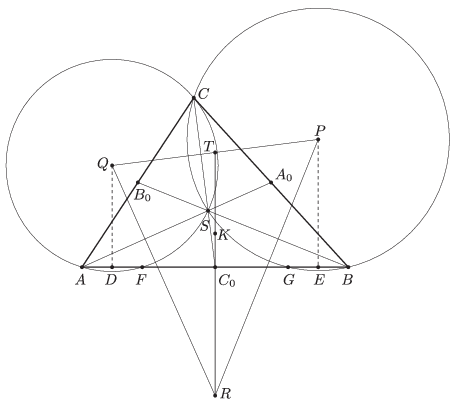
Jelölje az oldalak felezőpontjait az ábra szerint $\displaystyle A_0$, $\displaystyle B_0$ és $\displaystyle C_0$, valamint $\displaystyle PQ$-nak és $\displaystyle AB$ felezőmerőlegesének metszéspontját $\displaystyle T$. Ha megmutatjuk, hogy $\displaystyle T$ felezi a PQ szakaszt, akkor bebizonyítottuk az állítást. Vetítsük a $\displaystyle PQ$ szakaszt merőlegesen $\displaystyle AB$-re, $\displaystyle P$ és $\displaystyle Q$ képe legyen rendre $\displaystyle E$, illetve $\displaystyle D$. $\displaystyle T$ képe nyilván $\displaystyle C_0$, amivel $\displaystyle AB$ felezőpontját jelöltük. Amennyiben $\displaystyle T$ felezőpont, $\displaystyle C_0$ felezi $\displaystyle ED$-t is, amiből $\displaystyle {AD = EB}$. Megfordítva: ha ez igaz, a feladat állítása is igaz.

A $\displaystyle CS$ egyenes az $\displaystyle ACS$ és $\displaystyle BCS$ háromszögek köré írt körök közös húrja, vagyis hatványvonala. Emiatt $\displaystyle C_0$-nak a két körre vonatkozó hatványa ugyanakkora, vagyis a körök $\displaystyle AB$-vel vett második metszéspontját $\displaystyle G$-vel és $\displaystyle F$-el jelölve:

$\displaystyle C_0F\cdot C_0A = C_0G\cdot C_0B.$

Mivel $\displaystyle C_0A = C_0B \ne 0$, leoszthatunk vele. Azt kapjuk, hogy $\displaystyle C_0F = C_0G$. Mivel $\displaystyle C_0$ felezőpont, ebből következik, hogy $\displaystyle AF = BG$. $\displaystyle AF$ és $\displaystyle BG$ rendre az $\displaystyle ACS$, illetve $\displaystyle BCS$ körök húrjai, így a $\displaystyle D$ és $\displaystyle E$ pontok felezik őket (mivel középpontból húrra bocsátott merőlegesek talppontjai). Tehát az $\displaystyle AF = BG$ egyenlőséget kettővel osztva kapjuk, hogy $\displaystyle AD = EB$. Ezzel pedig bebizonyítottuk az állítást.

Sárosdi Zsombor (Budapest, Németh László Gimn., 11. évf.)

Statisztika:

27 dolgozat érkezett.
5 pontot kapott:	Badacsonyi István András, Balogh Tamás, Bereczki Zoltán, Bingler Arnold, Bogár Blanka, Di Giovanni Márk, Dinev Georgi, Emri Tamás, Fonyó Viktória, Forrás Bence, Janzer Barnabás, Janzer Olivér, Maga Balázs, Makk László, Petrényi Márk, Sándor Krisztián, Sárosdi Zsombor, Simkó Irén, Somogyvári Kristóf, Szabó 524 Tímea, Tossenberger Tamás, Venczel Tünde.
4 pontot kapott:	Sagmeister Ádám.
3 pontot kapott:	1 versenyző.
1 pontot kapott:	1 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2013. áprilisi matematika feladatai