Problem B. 4613. (March 2014)

B. 4613. The rhombus A₁B₁C₁D₁ lies in the interior of a parallelogram ABCD. The vectors and have the same direction, and the vectors and also have the same direction. Show that ABCD is a rhombus if and only if the sum of the areas of quadrilaterals AA₁D₁D and BCC₁D₁ is equal to the sum of the areas of quadrilaterals ABB₁A₁ and CDD₁C₁.

(Problem by L. Longáver, Matlap, Kolozsvár)

(3 pont)

Deadline expired on April 10, 2014.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A feladat feltételei alapján az \(\displaystyle A_{1}B_{1}C_{1}D_{1}\) rombusz oldalai párhuzamosak az \(\displaystyle ABCD\) paralelogramma oldalaival. Használjuk az 1. ábra jelöléseit és legyen \(\displaystyle T_{ADD_{1}A_{1}}= T_{1}\), \(\displaystyle T_{ABB_{1}A_{1}}=T_{2}\), \(\displaystyle T_{BCC_{1}B_{1}}=T_{3}\), \(\displaystyle T_{CDD_{1}C_{1}}=T_{4}\), valamint \(\displaystyle m_{a}\) és \(\displaystyle m_{b}\) a paralelogramma megfelelő magasságai, \(\displaystyle T\) pedig a területe.

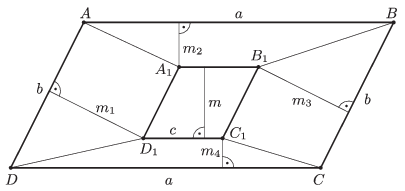
1. ábra

Ekkor \(\displaystyle T_{1}+T_{3}=T_{2}+T_{4}\) pontosan akkor teljesül, ha

\(\displaystyle \frac{(c+b)}{2}m_{1}+\frac{(c+b)}{2}m_{3}=\frac{(c+a)}{2}m_{2}+\frac{(c+a)}{2}m_{4}, \)

vagyis

\(\displaystyle \frac{(c+b)}{2}(m_{1}+m_{3}) =\frac{(c+a)}{2}(m_{2}+m_{4}), \quad\text{azaz}\)

\(\displaystyle (c+b)(m_{b}-m) =(c+a)(m_{a}-m).\)

Ez ekvivalens a \(\displaystyle cm_{b}+T-bm=cm_{a}+T-am\) egyenlőséggel. Ebből következik, hogy a szemközti területek összegének egyenlősége nem függ a rombusz helyzetétől.

Helyezzük a rombuszt a paralelogramma \(\displaystyle D\) csúcsához úgy, hogy \(\displaystyle D=D_{1}\) legyen.

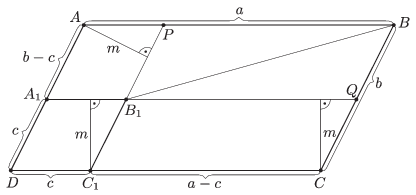
2. ábra

Ekkor az \(\displaystyle ABB_{1}A_{1}\) és \(\displaystyle BCC_{1}B_{1}\) trapézok területének egyenlőségét kell vizsgálni.

Húzzuk be a \(\displaystyle BPB_{1}Q\) paralelogramma \(\displaystyle BB_{1}\) átlóját. Ez felezi a paralelogramma területét, tehát elegendő az \(\displaystyle APB_{1}A_{1}\) és \(\displaystyle QCC_{1}B_{1}\) paralelogrammák területének egyenlőségét vizsgálni:

\(\displaystyle T_{APB_{1}A_{1}}=(b-c)\cdot m \quad\text{és}\quad T_{QCC_{1}B_{1}}=(a-c)\cdot m. \)

Így a két terület pontosan akkor egyenlő, ha \(\displaystyle (b-c)=(a-c)\), vagyis ha \(\displaystyle a=b\). Tehát az \(\displaystyle ABCD\) paralelogramma pontosan akkor rombusz, ha \(\displaystyle T_{1}+T_{3}=T_{2}{+T}_{4}\).

Szakács Lili Kata (Budapesti Fazekas M. Ált. Isk. és Gimn., 9. évf.) dolgozata alapján

Statistics:

114 students sent a solution.
3 points:	Andi Gabriel Brojbeanu, Andó Angelika, Babik Bálint, Balogh Menyhért, Baran Zsuzsanna, Baráth Míra Kincső, Berta Dénes, Cseh Kristóf, Csépai András, Csitári Nóra, Fekete Panna, Fellner Máté, Forrás Bence, Gál Hanna, Geng Máté, Győrfi-Bátori András, Gyulai-Nagy Szuzina, Hraboczki Attila Márton, Janzer Orsolya Lili, Kacz Dániel, Kátay Tamás, Kocsis Júlia, Kosztolányi Kata, Kovács 246 Benedek, Kovács 972 Márton, Kovács Balázs Marcell, Molnár-Sáska Zoltán, Nagy Gergely, Németh 777 Róbert, Németh Hanna, Pálfi Mária, Petrényi Márk, Rossen Péter, Sal Kristóf, Schrettner Bálint, Smodics Roland, Szabó Norbert, Szakács Lili Kata, Szűcs Kilián Ádám, Tóth Ádám Bars, Tóth Viktor, Vágó Ákos, Varga 123 Péter, Várkonyi Dorka, Várkonyi Lídia, Wiandt Péter, Williams Kada.
2 points:	40 students.
1 point:	22 students.
0 point:	4 students.
Unfair, not evaluated:	1 solutions.

Problems in Mathematics of KöMaL, March 2014