A B. 4623. feladat (2014. április)

B. 4623. Egy konvex négyszögben az átlók négy olyan háromszöget határoznak meg, amelyek területe egész szám. Bizonyítsuk be, hogy ennek a négy egésznek a szorzata nem végződhet 2014-re.

(3 pont)

A beküldési határidő 2014. május 12-én LEJÁRT.

Megoldás. Először megmutatjuk, hogy a két-két szemközti háromszög területének szorzata egyenlő. Jelölje a hároszögek területét az ábra szerint \(\displaystyle T_1\), \(\displaystyle T_2\), \(\displaystyle T_3\) és \(\displaystyle T_4\). A háromszögeknek az egyik átlóhoz tartozó magasságai legyenek \(\displaystyle m_1\) és \(\displaystyle m_2\), ennek az átlónak az átlók metszéspontja által meghatározott szakaszai pedig legyenek \(\displaystyle e_1\) és \(\displaystyle e_2\).

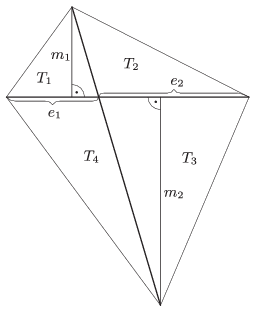
Ekkor

\(\displaystyle 2\,T_1=e_1m_1, \quad 2\,T_2=e_2m_1, \)

\(\displaystyle 2\,T_3=e_2m_2 \quad \text{és} \quad 2\,T_4=e_1m_2,\)

tehát

\(\displaystyle T_1T_3=\frac{e_1e_2m_1m_2}{4}=T_2T_4. \)

Ezért \(\displaystyle T_1T_2T_3T_4= {(T_1T_3)}^2\), vagyis a négy terület szorzata négyzetszám. Tudjuk, hogy a négyzetszámok 4-gyel osztva \(\displaystyle 0\) vagy \(\displaystyle 1\) maradékot adnak. Mivel a számok 4-es maradéka csak az utolsó két számjegyüktől függ, ezért ha egy szám \(\displaystyle 2014\)-re végződik, akkor a 4-es maradéka megegyezik a \(\displaystyle 14\)-nek a 4-es maradékával, azaz 2-vel. Tehát a területek szorzata nem végződhet \(\displaystyle 2014\)-re.

Varga Péter (Hajdúszoboszló, Hőgyes E. Gimn. és Szki., 10. évf.) dolgozata alapján

Statisztika:

125 dolgozat érkezett.
3 pontot kapott:	105 versenyző.
2 pontot kapott:	7 versenyző.
1 pontot kapott:	8 versenyző.
0 pontot kapott:	4 versenyző.
Nem versenyszerű:	1 dolgozat.

A KöMaL 2014. áprilisi matematika feladatai