A B. 4624. feladat (2014. április)

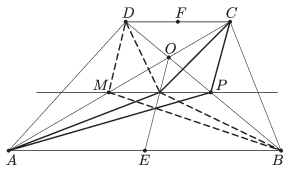
B. 4624. Az \(\displaystyle ABCD\) trapézban jelölje \(\displaystyle E\) és \(\displaystyle F\) az \(\displaystyle AB\), illetve \(\displaystyle CD\) alap felezőpontját, \(\displaystyle O\) pedig az átlók metszéspontját. Az \(\displaystyle OA\), \(\displaystyle OE\) és \(\displaystyle OB\) szakaszokat egy alapokkal párhuzamos egyenes rendre az \(\displaystyle M\), \(\displaystyle N\) és \(\displaystyle P\) pontokban metszi. Mutassuk meg, hogy az \(\displaystyle APCN\) és \(\displaystyle BNDM\) négyszögek területe egyenlő.

Javasolta: Longáver Lajos (Nagybánya)

(3 pont)

A beküldési határidő 2014. május 12-én LEJÁRT.

Megoldás. A négyszögeket az \(\displaystyle MN\), illetve \(\displaystyle NP\) átlók két-két háromszögre bontják, ezért

\(\displaystyle T_{APCN} =T_{APN}+T_{PCN} \quad\text{és}\)

\(\displaystyle T_{BNDM} =T_{BNM}+T_{NDM}.\)

Az \(\displaystyle MNP\) egyenes párhuzamos a trapéz alapjaival. Ebből egyrészt a párhuzamos szelőszakaszok tétele alapján

\(\displaystyle \frac{MN}{AE}=\frac{NP}{EB}, \quad \text{vagyis} \quad \frac{MN}{NP}=\frac{AE}{EB} \)

következik, s mivel \(\displaystyle E\) felezi az \(\displaystyle AB\) szakaszt, ezért kapjuk, hogy \(\displaystyle MN=NP\). Másrészt a párhuzamosság miatt a \(\displaystyle PCN\) és \(\displaystyle NDM\) háromszögek \(\displaystyle C\) illetve \(\displaystyle D\), valamint az \(\displaystyle APN\) és \(\displaystyle BNM\) háromszögek \(\displaystyle A\), illetve \(\displaystyle B\) csúcsaihoz tartozó magasságok is megegyeznek. Ezért

\(\displaystyle T_{APN}=T_{BNM} \quad \text{és} \quad T_{PCN}=T_{NDM}, \)

amiből a feladat állítása következik.

Nagy Odett (Szeged, Radnóti M. Gimn., 9. évf.) dolgozata alapján

Statisztika:

128 dolgozat érkezett.
3 pontot kapott:	111 versenyző.
2 pontot kapott:	9 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	4 versenyző.

A KöMaL 2014. áprilisi matematika feladatai