A B. 4674. feladat (2014. december)

B. 4674. Az \(\displaystyle ABC\) háromszög köré írt körön, a \(\displaystyle B\) csúcsot nem tartalmazó \(\displaystyle AC\) íven egy \(\displaystyle X\) pont mozog. Jelölje rendre \(\displaystyle Y\) és \(\displaystyle Z\) a \(\displaystyle BA\), illetve \(\displaystyle BC\) oldal \(\displaystyle A\)-n, illetve \(\displaystyle C\)-n túli meghosszabbításán azt a pontot, amelyre \(\displaystyle AY=AX\) és \(\displaystyle CZ=CX\). Mi az \(\displaystyle YZ\) szakasz felezőpontjának mértani helye?

Javasolta: Pozsonyi Enikő (Budapest)

(5 pont)

A beküldési határidő 2015. január 12-én LEJÁRT.

Megoldási ötlet: Keressünk olyan egybevágósági transzformációt, ami \(\displaystyle Y\)-t a \(\displaystyle Z\)-be viszi.

Megoldás. Legyen az \(\displaystyle YZ\) szakasz felezőpontja \(\displaystyle F\). Jelölje az \(\displaystyle A\) és \(\displaystyle Y\) pontok \(\displaystyle F\)-re vonatkozó tükörképét \(\displaystyle A'\) és \(\displaystyle Y'\). Ekkor \(\displaystyle Y'\equiv Z\). Mivel bármely szakasz párhuzamos a középpontos tükörképével, ezért \(\displaystyle A'Z\) párhuzamos \(\displaystyle AY\)-nal, s így \(\displaystyle AB\)-vel (1. ábra). Ezért ha az \(\displaystyle ABC\) háromszög \(\displaystyle B\)-nél lévő szöge \(\displaystyle \beta\), akkor \(\displaystyle A'ZB\sphericalangle = {180^{\circ}-\beta}\). Az \(\displaystyle ABCX\) négyszög húrnégyszög, ezért \(\displaystyle AXC\sphericalangle =180^{\circ}-ABC\sphericalangle = {180^{\circ}-\beta}\). Tehát az \(\displaystyle AXC\) és az \(\displaystyle A'ZC\) háromszögek egybevágóak, mert megegyezik egy szögük és az azt közrefogó két oldaluk, hiszen \(\displaystyle AX=AY=A'Z\) és \(\displaystyle CX=CZ\). Vagyis \(\displaystyle AC=A'C\), azaz a \(\displaystyle CA'A\) háromszög egyenlőszárú. Ezért alapjának \(\displaystyle F\) felezőpontját a \(\displaystyle C\) csúccsal összekötő egyenes az alap felezőmerőlegese, vagyis \(\displaystyle CF\) merőleges \(\displaystyle FA\)-ra. Tehát Thalész tételének megfordítása szerint \(\displaystyle F\) rajta van az \(\displaystyle AC\) szakasz \(\displaystyle k\) Thalész-körén.

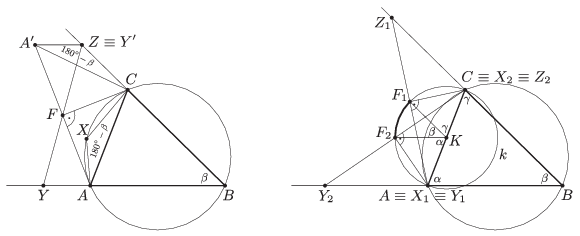
1. ábra                                                                       2. ábra

Meg kell még vizsgálnunk, hogy \(\displaystyle k\) mely pontjai állnak elő az \(\displaystyle YZ\) szakaszok felezőpontjaként. Legyen az \(\displaystyle ABC\) háromszög \(\displaystyle A\)-nál, illetve \(\displaystyle C\)-nél lévő szöge \(\displaystyle \alpha\), illetve \(\displaystyle \gamma\). Az \(\displaystyle X\) pont két szélső helyzete \(\displaystyle X_1\equiv A\) és \(\displaystyle X_2\equiv C\). Az első esetben \(\displaystyle Y_1\equiv A\) és \(\displaystyle F_1\) a \(\displaystyle CZ_1A\) egyenlőszárú háromszög \(\displaystyle Z_1A\) alapjának felezőpontja. Mivel \(\displaystyle Z_1CA\sphericalangle =180^{\circ}-\gamma\), ezért \(\displaystyle F_1CA\sphericalangle =90^{\circ}-\gamma /2\). Ugyanígy kapjuk, hogy ha \(\displaystyle X_2\equiv C\), akkor \(\displaystyle F_2AC\sphericalangle =90^{\circ}-\alpha /2\) (2. ábra). Ha \(\displaystyle k\) középpontja (\(\displaystyle AC\) felezőpontja) \(\displaystyle K\), akkor az \(\displaystyle F_1KC\) és az \(\displaystyle F_2KA\) egyenlőszárú háromszögekből azt kapjuk, hogy

\(\displaystyle F_1KC\sphericalangle =180^{\circ}- 2\cdot F_1CA\sphericalangle = 180^{\circ}- 2\cdot \left(90^{\circ}-\frac{\gamma }{2}\right) =\gamma, \)

és ugyanígy \(\displaystyle F_2KA\sphericalangle =\alpha\), ezért \(\displaystyle F_1KF_2\sphericalangle = 180^{\circ}-(\gamma +\alpha )=\beta\).

Ha \(\displaystyle X\) folytonosan mozog \(\displaystyle A\)-ból \(\displaystyle C\)-be, akkor \(\displaystyle F\) is nyilván folytonosan mozog \(\displaystyle F_1\)-ből \(\displaystyle F_2\)-be. Tehát a keresett mértani hely az \(\displaystyle AC\) szakasz Thalész körének a \(\displaystyle \beta \) középponti szögű \(\displaystyle F_1F_2\) íve.

Kocsis Júlia (Dunakeszi, Radnóti M. Gimn., 10. évf.) dolgozata alapján

Statisztika:

40 dolgozat érkezett.
5 pontot kapott:	Baran Zsuzsanna, Cseh Kristóf, Csépai András, Döbröntei Dávid Bence, Fekete Panna, Gáspár Attila, Katona Dániel, Kerekes Anna, Kocsis Júlia, Kovács 972 Márton, Kovács Péter Tamás, Nagy-György Pál, Porupsánszki István, Schrettner Bálint, Schwarcz Tamás, Szebellédi Márton, Tóth Viktor, Vághy Mihály, Varga-Umbrich Eszter, Wei Cong Wu, Williams Kada.
4 pontot kapott:	Lajkó Kálmán, Leitereg Miklós, Németh 123 Balázs, Szakács Lili Kata.
3 pontot kapott:	7 versenyző.
2 pontot kapott:	2 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	3 versenyző.

A KöMaL 2014. decemberi matematika feladatai