A B. 4714. feladat (2015. május)

B. 4714. Adott a síkon 2015 pont. Mutassuk meg, hogy ha közülük bármely négy egy konvex négyszög négy csúcsa, akkor a pontok egy konvex 2015-szög csúcsai.

(4 pont)

A beküldési határidő 2015. június 10-én LEJÁRT.

Megoldás. A 2015 pont akkor alkot konvex \(\displaystyle 2015\)-szöget, ha közülük semelyik 3 nem esik egy egyenesbe és mindegyikük rajta van a konvex burkuk határán.

Az adott pontok közül semelyik három nem eshet egy egyenesbe, mert akkor a három kollineáris ponthoz egy tetszőleges negyediket választva négy olyan pontot kapnánk, amik nem alkotnak konvex négyszöget.

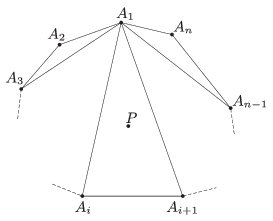
Tegyük fel, hogy a pontok nem egy konvex \(\displaystyle 2015\)-szög csúcsai. Mivel a pontok nem esnek egy egyenesre, ezért ekkor konvex burkuk, \(\displaystyle \mathcal{K}\), egy konvex \(\displaystyle n\)-szög valamely \(\displaystyle n<2015\) egészre, továbbá a pontok közül legalább egy \(\displaystyle \mathcal{K}\) belsejébe esik. Válasszuk ki \(\displaystyle \mathcal{K}\) egyik csúcsát (az ábrán \(\displaystyle A_1\)), és húzzuk be az ebből kiinduló \(\displaystyle n-3\) darab átlót. Ezek \(\displaystyle \mathcal{K}\)-t \(\displaystyle n-2\) darab háromszögre osztják, s e háromszögek teljesen lefedik \(\displaystyle \mathcal{K}\)-t. Ezért ha \(\displaystyle P\) olyan pont a \(\displaystyle 2015\) közül, mely \(\displaystyle \mathcal{K}\) belsejébe esik, akkor az átlók által meghatározott \(\displaystyle n-2\) háromszög között van egy olyan (az ábrán \(\displaystyle A_1A_iA_{i+1}\)), amelyiknek a belsejébe esik. Ekkor viszont \(\displaystyle P\) és az azt tartalmazó háromszög három csúcsa nem alkot konvex négyszöget. Ez az ellentmondás bizonyítja állításunkat.

Nagy Dávid Paszkál (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 9. évf.) dolgozata alapján

Statisztika:

80 dolgozat érkezett.
4 pontot kapott:	55 versenyző.
3 pontot kapott:	8 versenyző.
2 pontot kapott:	6 versenyző.
1 pontot kapott:	3 versenyző.
0 pontot kapott:	8 versenyző.

A KöMaL 2015. májusi matematika feladatai