A B. 4716. feladat (2015. május)

B. 4716. Az \(\displaystyle ABCDE\) szabályos ötszögből kivágtuk az \(\displaystyle AB\) és \(\displaystyle AE\) élek által meghatározott \(\displaystyle ABFE\) rombuszt. Határozzuk meg a megmaradó \(\displaystyle BCDEF\) konkáv ötszöglemez súlypontját.

Javasolta: Dombi Péter (Pécs)

(3 pont)

A beküldési határidő 2015. június 10-én LEJÁRT.

Megoldásvázlat: A \(\displaystyle BCDEF\) ötszög felbontható a \(\displaystyle BCF\) és \(\displaystyle ECD\) háromszögekre. A keresett \(\displaystyle S\) súlypont a szimmetria miatt illeszkedik az \(\displaystyle AF\) egyenesre. A \(\displaystyle BCF\) és az \(\displaystyle ECD\) háromszögek súlypontját összekötő egyenesre is illeszkedik a súlypont, és erről az egyenesről belátható, hogy átmegy \(\displaystyle F\)-en. Így \(\displaystyle S\) maga az \(\displaystyle F\) pont.

Megoldás. A megoldás során fel fogjuk használni a következő, ismert állítást.

Lemma. Ha egy síkidomot két részre osztunk, a részek területei \(\displaystyle T_1\) és \(\displaystyle T_2\), súlypontjaik pedig \(\displaystyle S_1\) és \(\displaystyle S_2\), akkor a síkidom \(\displaystyle S\) súlypontja az \(\displaystyle S_1S_2\) szakasznak az a pontja, melyre \(\displaystyle T_1:T_2=S_2S:SS_1\) teljesül.

Tudjuk, hogy a szabályos ötszög átlója párhuzamos az ötszög szemközti oldalával. Mivel a rombusz szemközti oldalai is párhuzamosak s egy adott ponton át egy adott egyenessel csak egy párhuzamos húzható, ezért \(\displaystyle F\) megegyezik az \(\displaystyle EC\) és \(\displaystyle BD\) átlók metszéspontjával.

Legyen a \(\displaystyle BCDEF\) ötszöglemez súlypontja \(\displaystyle S\). Ha a lemezt a \(\displaystyle CD\) szakasz \(\displaystyle f\) felezőmerőlegesével osztjuk két részre, akkor a részek \(\displaystyle f\)-re nézve szimmetrikusak, tehát súlypontjaik is azok, amiből a lemma miatt következik, hogy \(\displaystyle S\) rajta van \(\displaystyle f\)-en.

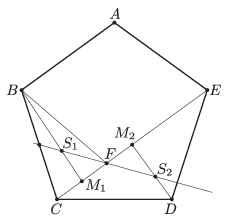
centerline1. ábra

Osszuk most az ötszöglemezt az \(\displaystyle EC\) egyenessel két részre. Az így keletkezett két háromszög, \(\displaystyle BCF\) és \(\displaystyle DEC\) egyenlőszárú, mert a rombusz oldalainak egyenlősége miatt \(\displaystyle BF=AE\), tehát mindkét háromszögnek van két-két olyan oldala, melyek hossza megegyezik a szabályos ötszög oldalának hosszával. Legyen a \(\displaystyle CF\), illetve \(\displaystyle CE\) szakaszok felezőpontja \(\displaystyle M_1\), illetve \(\displaystyle M_2\), a \(\displaystyle BCF\) és \(\displaystyle DEC\) háromszögek súlypontja pedig \(\displaystyle S_1\), illetve \(\displaystyle S_2\) (1. ábra). Mivel bármely háromszögben a súlypont harmadolja a súlyvonalakat, ezért ekkor \(\displaystyle S_1\) a \(\displaystyle BM_1\), \(\displaystyle S_2\) pedig a \(\displaystyle DM_2\) szakasz \(\displaystyle EC\) egyeneshez közelebbi harmadolópontja. Mivel a két háromszög egyenlő szárú, így \(\displaystyle BM_1\perp CF\) és \(\displaystyle DM_2\perp CE\). Ezért annál a merőleges tengelyes affinitásnál, melynek tengelye az \(\displaystyle EC\) egyenes, aránya pedig \(\displaystyle 1/3\), a \(\displaystyle B\) pont képe \(\displaystyle S_1\), a \(\displaystyle D\) pont képe \(\displaystyle S_2\), a tengelyen lévő \(\displaystyle F\) pont képe pedig önmaga lesz. Ezért az affinitásnál a \(\displaystyle BFD\) egyenes képe az \(\displaystyle S_1FS_2\) egyenes lesz, azaz \(\displaystyle S_1S_2\) átmegy \(\displaystyle F\)-en.

A lemma miatt a konkáv ötszöglemez súlypontja az \(\displaystyle S_1S_2\) szakaszon is rajta van, tehát nem lehet más, mint \(\displaystyle f\) és \(\displaystyle S_1S_2\) metszéspontja. Vagyis a \(\displaystyle BCDEF\) konkáv ötszöglemez súlypontja az \(\displaystyle F\) pont.

Sal Kristóf (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 11. évf.) dolgozatát felhasználva

Statisztika:

62 dolgozat érkezett.
3 pontot kapott:	Andó Angelika, Kocsis Júlia, Kuchár Zsolt, Tóth Viktor.
2 pontot kapott:	Bereczki Zoltán, Cseh Kristóf, Csorba Benjámin, Dobák Dávid, Gál Hanna, Glasznova Maja, Hansel Soma, Horeftos Leon, Khayouti Sára, Kovács 246 Benedek, Leitereg Miklós, Nagy 555 Botond, Nagy-György Zoltán, Páli Petra, Schrettner Bálint, Simon Dániel Gábor, Stein Ármin, Széles Katalin, Török Tímea, Török Zsombor Áron, Váli Benedek, Varga-Umbrich Eszter, Várkonyi Dorka, Wiandt Péter.
1 pontot kapott:	27 versenyző.
0 pontot kapott:	4 versenyző.
Nem versenyszerű:	3 dolgozat.

A KöMaL 2015. májusi matematika feladatai