A B. 4718. feladat (2015. május)

B. 4718. Az $\displaystyle ABCDA'B'C'D'$ kocka $\displaystyle B'C'$ élének felezőpontja $\displaystyle E$, $\displaystyle C'D'$ élének felezőpontja pedig $\displaystyle F$. Az $\displaystyle AEF$ sík két részre osztja a kockát. Határozzuk meg a két rész térfogatának arányát.

(5 pont)

A beküldési határidő 2015. június 10-én LEJÁRT.

Megoldás. Legyen a kocka éle egységnyi. Az $\displaystyle AEF$ sík és az $\displaystyle A'B'$ egyenes metszéspontja a $\displaystyle G$, az $\displaystyle A'D'$ egyenes és a sík metszéspontja a $\displaystyle H$ pont. A metszéspontok léteznek, mert a sík egyik egyenessel sem párhuzamos. Legyen továbbá az $\displaystyle AEF$ sík metszéspontja a $\displaystyle BB'$ és a $\displaystyle DD'$ egyenesekkel rendre az $\displaystyle I$ és a $\displaystyle J$ pont. Ekkor a kockából az $\displaystyle AEF$ síkkal lemetszett, az $\displaystyle A'$ pontot tartalmazó rész térfogatát megkapjuk, ha az $\displaystyle AA'GH$ tetraéder térfogatából levonjuk a $\displaystyle B'GIE$ és a $\displaystyle D'HJF$ tetraéder térfogatát.

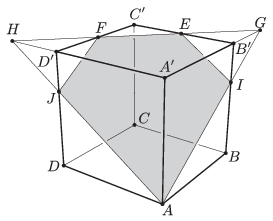
$\displaystyle EC'F$ egyenlő szárú derékszögű háromszög, ezért $\displaystyle HFD'\sphericalangle=EFC'\sphericalangle=45^{\circ}$, tehát a $\displaystyle HD'F$ derékszögű háromszög is egyenlő szárú. Ekkor $\displaystyle HD'=D'F=\frac{1}{2}$, így $\displaystyle HA'=\frac{3}{2}$. Az $\displaystyle AHA'$ szögre tekintve a párhuzamos szelőszakaszok tételét:

$\displaystyle JD'=AA'\cdot\frac{HD'}{HA'}=1\cdot\frac{1}{2}:\frac{3}{2}=\frac{1}{3}.$

Az előbbivel egyező gondolatmenettel $\displaystyle GEB'\sphericalangle=FEC'\sphericalangle=45^{\circ}$, illetve $\displaystyle B'G= B'E=\frac{1}{2}$ és $\displaystyle B'I=\frac{1}{3}$.

Az $\displaystyle AA'GH$ tetraéder $\displaystyle A'$ pontba futó élei páronként merőlegesek, így a tetraéder térfogata

$\displaystyle V_{AA'GH}=\frac{3}{2}\cdot \frac{3}{2}\cdot \frac{1}{2}\cdot \frac{1}{3}=\frac{3}{8}\, \text{ térfogategység.}$

Szintén páronként merőlegesek a $\displaystyle B'GIE$ tetraéder $\displaystyle B'$ csúcsból kiinduló élei. Ezek hosszának ismeretében a térfogata:

$\displaystyle V_{B'GIE}=\frac{1}{2}\cdot \frac{1}{2}\cdot \frac{1}{2}\cdot \frac{1}{3}\cdot\frac{1}{3}=\frac{1}{72}.$

Az ezzel egybevágó $\displaystyle D'HJF$ tetraéder térfogata is $\displaystyle \frac{1}{72}$ térfogategység.

Az eddigiek alapján az $\displaystyle AEF$ síkkal lemetszett, az $\displaystyle A'$ pontot tartalmazó rész térfogata:

$\displaystyle V_{AA'GH}-V_{B'GIE}-V_{D'HJF}=\frac{3}{8}-\frac{1}{72}-\frac{1}{72}=\frac{25}{72}.$

A másik rész ennek megfelelően $\displaystyle \frac{47}{72}$, végül a két rész térfogatának aránya $\displaystyle 25: 47$.

Öreg Botond (Budapesti Fazekas M. Gyak. Ált. Isk. és Gimn., 12. évf.) dolgozata alapján

Statisztika:

57 dolgozat érkezett.
5 pontot kapott:	Andi Gabriel Brojbeanu, Andó Angelika, Baran Zsuzsanna, Cseh Kristóf, Csépai András, Döbröntei Dávid Bence, Fekete Panna, Gáspár Attila, Glasznova Maja, Hansel Soma, Kocsis Júlia, Kosztolányi Kata, Lajkó Kálmán, Nagy Dávid Paszkál, Nagy Kartal, Nagy-György Pál, Nagy-György Zoltán, Németh 123 Balázs, Öreg Botond, Polgár Márton, Porupsánszki István, Schrettner Bálint, Schwarcz Tamás, Somogyi Pál, Szebellédi Márton, Vághy Mihály, Váli Benedek, Várkonyi Dorka, Wiandt Péter, Williams Kada.
4 pontot kapott:	Bereczki Zoltán, Gál Hanna, Imolay András, Molnár-Sáska Zoltán, Sal Kristóf, Szakály Marcell, Szemerédi Levente, Tóth Viktor, Vu Mai Phuong, Zolomy Kristóf.
3 pontot kapott:	8 versenyző.
2 pontot kapott:	3 versenyző.
1 pontot kapott:	4 versenyző.
0 pontot kapott:	2 versenyző.

A KöMaL 2015. májusi matematika feladatai