A B. 4721. feladat (2015. május)

B. 4721. A $\displaystyle k$ kör érinti az $\displaystyle ABC$ egyenlő szárú háromszög $\displaystyle AB$ és $\displaystyle AC$ szárait, a $\displaystyle BC$ alapját pedig $\displaystyle K$-ban és $\displaystyle L$-ben metszi. Az $\displaystyle AK$ szakasz a $\displaystyle k$ kört másodszor az $\displaystyle M$ pontban metszi. A $\displaystyle K$ pont $\displaystyle B$-re, illetve $\displaystyle C$-re vonatkozó tükörképe rendre $\displaystyle P$ és $\displaystyle Q$. Igazoljuk, hogy $\displaystyle k$ érinti a $\displaystyle PMQ$ háromszög köré írt kört.

(6 pont)

A beküldési határidő 2015. június 10-én LEJÁRT.

Megoldás. Használjuk az ábra jelöléseit, vagyis legyen a $\displaystyle k$ kör középpontja az $\displaystyle O$ pont, az $\displaystyle AB$ és $\displaystyle AC$ szárakon az érintési pontok rendre $\displaystyle D$ és $\displaystyle E$, továbbá jelölje az $\displaystyle MK$ szakasz felezőpontját $\displaystyle F$.

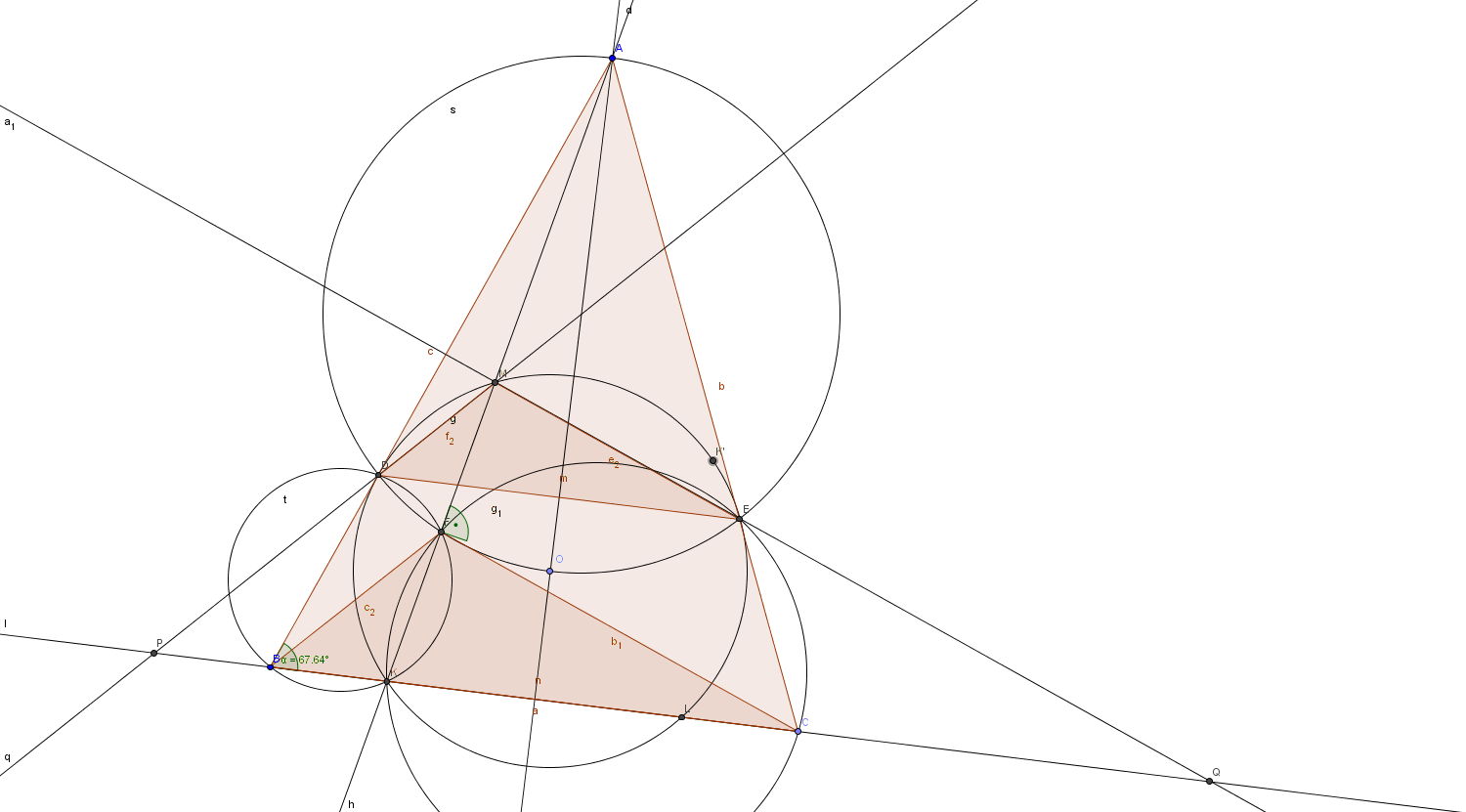
A feladat annak igazolását kéri, hogy a $\displaystyle k$ kör és a $\displaystyle PMQ$ kör érinti egymást. Nyilván mindkét kör tartalmazza az $\displaystyle M$ pontot, tehát azt kell igazolnunk, hogy $\displaystyle M$-ben érinti egymást a két kör. Ezt a következőképp igazoljuk: azt fogjuk belátni, hogy a $\displaystyle DME$ és a $\displaystyle PMQ$ háromszögek hasonlóak egymáshoz, méghozzá úgy, hogy egy $\displaystyle M$ középpontú, $\displaystyle \frac{PQ}{DE}$ arányú középpontú nagyítás a $\displaystyle DME$ háromszöget a $\displaystyle PMQ$ háromszögbe viszi át. Ekkor ugyanis a két háromszög köré írt körét is ugyanilyen nyújtás viszi egymásba. Ismert, és könnyen belátható tétel, hogy ha a $\displaystyle k$ kört egy, a körvonalon lévő $\displaystyle M$ középpontú nagyítással transzformáljuk, akkor a $\displaystyle k'$ kép a $\displaystyle k$ kört $\displaystyle M$-ben érinti, hiszen $\displaystyle M$ a transzformáció során fixpont, más fixpont azonban nincs.

Tehát a továbbiakban azt látjuk be, hogy a $\displaystyle PMQ$ és $\displaystyle DEF$ háromszögek a fönt leírt módon hasonlóak. Ehhez vegyük észre, hogy csupán annyi szükséges, hogy az $\displaystyle M$, $\displaystyle D$, $\displaystyle P$ illetve $\displaystyle M$, $\displaystyle E$, $\displaystyle Q$ pontok egy egyenesen legyenek. Ekkor ugyanis nyilvánvalóan a két háromszög három oldala páronként párhuzamos: $\displaystyle DE||BC$ könnyen igazolható, ha összevetjük a külső pontból húzott érintőszakaszok tételét a párhuzamos szelők tételének megfordításával, hiszen az előbbi szerint $\displaystyle AD=AE$, s mivel $\displaystyle ABC$ egyenlő szárú, így $\displaystyle AB=AC$. A párhuzamos szelők tételének megfordítása szerint ha $\displaystyle \frac{AB}{AD}=\frac{AC}{AE}$, ami igaz, akkor $\displaystyle DE||BC$. Mivel pedig feltettük, hogy az $\displaystyle M$, $\displaystyle D$, $\displaystyle P$ és $\displaystyle M$, $\displaystyle E$, $\displaystyle Q$ pontok kollineárisak, így $\displaystyle MD||MP$ és $\displaystyle ME||MQ$. Tehát a két háromszög hasonló. A hasonlóság aránya $\displaystyle \frac{DE}{PQ}$, így $\displaystyle MD=\frac{DE}{PQ}\cdot MP$, hasonlóan $\displaystyle ME=\frac{DE}{PQ}\cdot MQ$, és így már könnyen látszik, hogy a fönt vizsgált transzformáció egymásba viszi a két háromszöget és a köré írt körüket is.

Összefoglalva az eddigieket: elegendő azt igazolnunk, hogy az $\displaystyle M$, $\displaystyle D$, $\displaystyle P$, valamint az $\displaystyle M$, $\displaystyle E$, $\displaystyle Q$ pontok kollineárisak.

Most igazoljuk azt, hogy ha az $\displaystyle ABC$ háromszög alapon fekvő szöge $\displaystyle \alpha$, akkor $\displaystyle DME\angle=180°-\alpha$. Nyilván $\displaystyle ADE\angle=\alpha$, hiszen egyállású $\displaystyle ABC\angle$-gel. Az $\displaystyle ADE\angle$ a $\displaystyle k$ körben a $\displaystyle DE$ húrhoz tartozó érintő szárú kerületi szög. A kerületi szögek tétele miatt $\displaystyle DKE\angle=ADE\angle=\alpha$. Az $\displaystyle M$ pont a $\displaystyle DE$ húr másik oldalán helyezkedik el, emiatt $\displaystyle DME\angle=180°-\alpha$

Azt fogjuk belátni, hogy $\displaystyle PME\angle=DME\angle$, ebből nyilván következik a bizonyítandó. Épp az imént bizonyítottuk be, hogy $\displaystyle DME\angle=180°-\alpha$, vagyis csak annyit kell látnunk, hogy $\displaystyle PME\angle=180°-\alpha$. Ez ekvivalens azzal, hogy a $\displaystyle PMEC$ négyszög húrnégyszög, hiszen $\displaystyle ECP\angle=\alpha$.

Tehát azt fogjuk igazolni, hogy $\displaystyle PMEC$ húrnégyszög. Ehhez az kell, hogy:

$\displaystyle CPM\angle+MEC\angle=180°$

Triviálisan $\displaystyle CPM\angle=KPM\angle$. Ha a $\displaystyle KPM\angle$ szöget $\displaystyle K$ középponttal $\displaystyle \frac12$ aránnyal kicsinyítjük, a kép éppen a $\displaystyle KBF\angle$ lesz. A középpontos hasonlóság szögtartó, így $\displaystyle KBF\angle=KPM\angle=CPM\angle$, vagyis elég azt látnunk, hogy:

$\displaystyle KBF\angle+MEC\angle=180°$

Nyilván ez ekvivalens a következővel:

$\displaystyle KBF\angle=MEA\angle$

Az $\displaystyle MEA\angle$ szög a $\displaystyle k$ körben az $\displaystyle ME$ húrhoz tartozó érintő szárú kerületi szög, vagyis:

$\displaystyle MEA\angle=MDE\angle$

Összevetve a föntivel:

$\displaystyle KBF\angle=MDE\angle$

Ezt úgy fogjuk igazolni, hogy belátjuk: a két szög egyállású. Nyilván $\displaystyle DE||BC$ triviális, csak a $\displaystyle DM||BF$ szorul bizonyításra.

Ehhez néhány húrnégyszögre lesz szükségünk. A $\displaystyle DFEA$ négyszögről fogjuk elsőként bebizonyítani, hogy húrnégyszög. Az $\displaystyle AED$ háromszög köré írt kör valójában az $\displaystyle AO$ szakasz Thalész-köre: hiszen az érintés miatt $\displaystyle ODA\angle=AEO\angle=90°$. Tehát csak annyit kell látnunk, hogy $\displaystyle AFO\angle=90°$, amihez nyilván elegendő $\displaystyle OFK\angle=90°$. Tükrözzük az $\displaystyle OFK\angle$ szöget középpontosan $\displaystyle K$-ra! Ekkor $\displaystyle F$ képe $\displaystyle M$ lesz, $\displaystyle K$ helyben marad, $\displaystyle O$ képe pedig $\displaystyle K'$ lesz. A szögtartás miatt $\displaystyle OFK\angle=K'MK\angle$. Könnyen látszik, hogy $\displaystyle K'$, $\displaystyle M$ és $\displaystyle K$ mind a $\displaystyle k$ kör pontjai, ráadásul $\displaystyle KK'$ egy átmérő a $\displaystyle k$ körben, így Thalész tétele miatt $\displaystyle K'MK\angle=90°$, amivel igazoltuk segédállításunkat.

Tehát $\displaystyle DFEA$ húrnégyszög, emiatt $\displaystyle DFE\angle=180°-EAD\angle=180°-(180°-2\alpha)=2\alpha$. Mivel $\displaystyle AD=AE$, azért $\displaystyle DFA\angle=AFE\angle=\frac{DFE\angle}{2}=\alpha$. Emiatt $\displaystyle KFD\angle=EFK\angle=180°-\alpha$. Felhasználva, hogy $\displaystyle DBK\angle=KCE\angle=\alpha$, kapjuk, hogy $\displaystyle BKFD$, valamint $\displaystyle KCEF$ is húrnégyszög. Felírva az $\displaystyle A$ pont $\displaystyle BKFD$ köré írt körére vonatkozó hatványát:

$\displaystyle AD\cdot AB=AF\cdot AK$

Felírva az érintő és szelőszakaszok tételét az $\displaystyle A$ pontra és a $\displaystyle k$ körre:

$\displaystyle AD^2=AM\cdot AK$

$\displaystyle AK=\frac{AD^2}{AM}$

Ezt beírva a hatványra vonatkozó egyenletbe:

$\displaystyle AD\cdot AB=AF\cdot\frac{AD^2}{AM}$

Rendezve:

$\displaystyle \frac{AB}{AD}=\frac{AF}{AM}$

A párhuzamos szelők tételének megfordítása miatt így:

$\displaystyle BF||MD$

Éppen ezt akartuk látni. Nyilván teljesen analóg módon bizonyítjuk azt, hogy $\displaystyle DME\angle=DMQ\angle$, szimmetria okokból. Ezzel a bizonyítást befejeztük.

Németh Balázs (Budapesti Fazekas M . Gyak. Ált. Isk. és Gimn., 9. évf.)

Statisztika:

16 dolgozat érkezett.
6 pontot kapott:	Andó Angelika, Cseh Kristóf, Csépai András, Fekete Panna, Glasznova Maja, Nagy-György Pál, Németh 123 Balázs, Schrettner Bálint, Schwarcz Tamás, Szebellédi Márton, Török Tímea, Williams Kada.
5 pontot kapott:	Andi Gabriel Brojbeanu.
4 pontot kapott:	1 versenyző.
3 pontot kapott:	1 versenyző.
2 pontot kapott:	1 versenyző.

A KöMaL 2015. májusi matematika feladatai