A B. 4724. feladat (2015. szeptember)

B. 4724. Oldjuk meg és ábrázoljuk az

\(\displaystyle x+y-xy+\frac{1}{x} +\frac{1}{y} -\frac{1}{xy}\le 2 \)

egyenlőtlenséget.

(4 pont)

A beküldési határidő 2015. október 12-én LEJÁRT.

Megoldásvázlat. Írjuk át az egyenlőtlenséget a következő alakba:

\(\displaystyle 0\leq xy+1-x-\frac{1}{y}-y-\frac{1}{x}+1+\frac{1}{xy}.\)

Ekkor mindent közös nevezőre hozva, a számlálóból kiemelhető \(\displaystyle (xy+1)\), sőt, a kapott kifejezés még tovább bontható, így a következő alakhoz jutunk:

\(\displaystyle 0 \leq \frac{(x-1)(y-1)(xy+1)}{xy}\).

A megoldáshoz egy egyszerű előjel vizsgálatra van szükség, érdemes kilenc esetet külön vizsgálni aszerint, hogy \(\displaystyle x\), illetve \(\displaystyle y\) negatív, \(\displaystyle 0\) és \(\displaystyle 1\) között van-e (\(\displaystyle 0\)-nál nem értelmes a kifejezés, így azzal nem foglalkozunk tovább), vagy \(\displaystyle 1\)-nél nagyobb (az \(\displaystyle 1\)-et is beleértve).

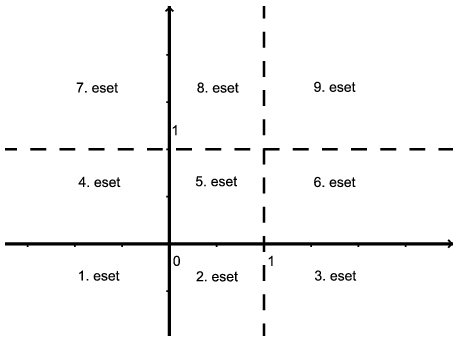
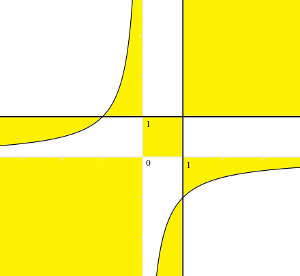
Az 1., 5., 6., 8. és 9. eset könnyű, hiszen ezeknél mindegyik szorzótényezőről egyértelműen eldönthető, hogy pozitív, vagy negatív-e, így az 1., 5. és 9. esetben látjuk, hogy minden \(\displaystyle (x;y)\) számpár megfelel, míg a 6. és 8. esetekben egy számpár sem jó. A maradék négy esetben keletkezik újabb feltétel: ha \(\displaystyle 0 < x < 1\), valamint \(\displaystyle y < 0\) (2. eset), akkor \(\displaystyle (x-1)<0; (y-1)<0; xy<0\), így \(\displaystyle (xy+1)\leq0\) kell, hogy teljesüljön. Ez azt jelenti, hogy \(\displaystyle y\leq-\frac{1}{x}\). Hasonlóan a 3. esetre az \(\displaystyle y\geq-\frac{1}{x}\) feltételt kapjuk, míg a 4. és 7. esetekre éppen ezek fordítottjait. Ezek alapján a 2. ábra szemlélteti a megoldásokat a valós számpárok halmazán. (A képen a sötét színnel jelzett határok igen, míg a világosak nem tartoznak hozzá a megoldáshalmazhoz.)

Statisztika:

157 dolgozat érkezett.
4 pontot kapott:	97 versenyző.
3 pontot kapott:	19 versenyző.
2 pontot kapott:	21 versenyző.
1 pontot kapott:	17 versenyző.
0 pontot kapott:	3 versenyző.

A KöMaL 2015. szeptemberi matematika feladatai