 |
A B. 4833. feladat (2016. december) |
B. 4833. Az \(\displaystyle R\) sugarú kör félkörnél kisebb körcikkébe beírt kör sugara \(\displaystyle r\), a körcikket határoló körív végpontjait összekötő húr hossza \(\displaystyle 2a\). Igazoljuk, hogy
\(\displaystyle \frac 1r= \frac 1R+ \frac 1a. \)
(3 pont)
A beküldési határidő 2017. január 10-én LEJÁRT.
Megoldás. Legyen a körív középpontja \(\displaystyle K\), az ív két végpontja \(\displaystyle A\) és \(\displaystyle B\), az ív felezőpontja \(\displaystyle F\), a beírt kör középpontja az \(\displaystyle O\) pont, s végül a beírt kör érintési pontja a \(\displaystyle BK\) sugáron az \(\displaystyle E\) pont.
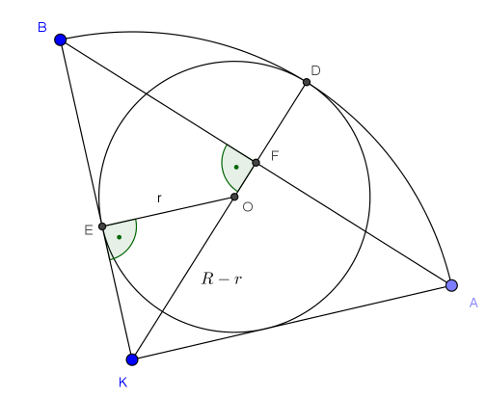
A \(\displaystyle BFK\) és \(\displaystyle OEK\) derékszögű háromszögek hasonlók, mert egyik hegyesszögük egybeeesik. Írjuk fel a megfelelő oldalak arányának egyenlőségét:
\(\displaystyle \frac{OE}{BF}=\frac{OK}{BK}.\)
Ugyanez a feladat szövegében szereplő jelölésekkel:
\(\displaystyle \frac{r}{a}=\frac{R-r}{R}.\)
Beszorzás és rendezés után
\(\displaystyle rR=aR-ar,\)
\(\displaystyle aR=rR+ar.\)
Elosztva az egyenlőség mindkét oldalát \(\displaystyle arR\)-rel éppen a bizonyítandó állítást kapjuk:
\(\displaystyle \frac{1}{r}=\frac{1}{R}+\frac{1}{a}.\)
Statisztika:
122 dolgozat érkezett. 3 pontot kapott: 118 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 1 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2016. decemberi matematika feladatai

