 |
A B. 4834. feladat (2016. december) |
B. 4834. Legyen az \(\displaystyle ABC\) hegyesszögű háromszög köréírt körének középpontja a \(\displaystyle K\) pont. A \(\displaystyle K\)-n keresztül \(\displaystyle AB\)-vel húzott párhuzamos egyenes a \(\displaystyle BC\) egyenest a \(\displaystyle D\), a \(\displaystyle CA\) egyenest pedig az \(\displaystyle E\) pontban metszi. Hasonlóan, a \(\displaystyle K\)-n keresztül a \(\displaystyle BC\)-vel húzott párhuzamosnak a \(\displaystyle CA\) egyenessel vett metszéspontja az \(\displaystyle F\), a \(\displaystyle BA\) egyenessel vett metszéspontja pedig a \(\displaystyle G\) pont. Igazoljuk, hogy az \(\displaystyle E\) középpontú \(\displaystyle EA\) sugarú, az \(\displaystyle F\) középpontú \(\displaystyle FC\) sugarú, valamint az \(\displaystyle ABC\) háromszög köré írt kör egy pontban metszik egymást.
Javasolta: Miklós Szilárd (Herceghalom)
(4 pont)
A beküldési határidő 2017. január 10-én LEJÁRT.
Megoldás. Jelöljük az ábra alapján az \(\displaystyle ABK\) egyenlő szárú háromszög alapon fekvő szögeit \(\displaystyle δ\)-val, a \(\displaystyle BCK\) egyenlő szárú háromszög alapon fekvő szögeit pedig \(\displaystyle ε\)-nal.
Mivel \(\displaystyle ED‖AB\), azért BAK∡=AKE∡=δ és ABK∡=BKD∡=δ, mert váltószögek.
Hasonlóan, mivel GF‖BC, azért CBK∡=BKG∡=ε és BCK∡=CKF∡=ε, mert váltószögek.
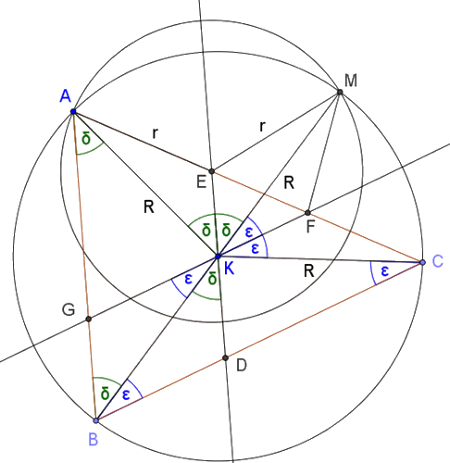
Legyen a K középpontú KA=R sugarú és az E középpontú EA=r sugarú körök metszéspontja M.
Ekkor az AKEΔ és az MKEΔ egybevágó, mert EK oldaluk közös, KA=KM=R és EA=EM=r. Ezért EKM∡=AKE∡=δ.
Mivel GKD∡=δ+ε=EKF∡, mert csúcsszögek, így MKF∡=EKF∡-δ=ε.
Az MKFΔ és a CKFΔ egybevágó, mert KF oldaluk közös, KM=KC=R és MKF∡=CKF∡=ε, így megegyeznek két oldalban és a közbezárt szögben.
Az egybevágóság miatt FM=FC, így M pont rajta van az F középpontú FC sugarú körön is, vagyis a három kör egy pontban metszi egymást.
Statisztika:
73 dolgozat érkezett. 4 pontot kapott: 65 versenyző. 3 pontot kapott: 5 versenyző. 2 pontot kapott: 2 versenyző. 0 pontot kapott: 1 versenyző.
A KöMaL 2016. decemberi matematika feladatai

